Two efficient algorithms for computing the characteristics of a subsegment of a digital straight line

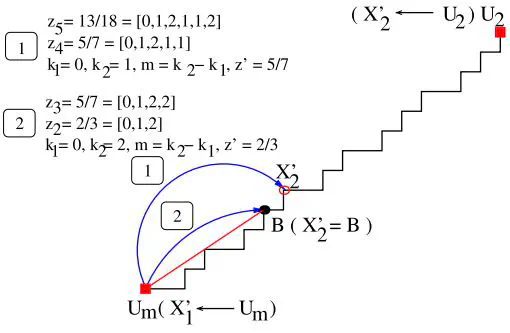
Abstract

We address the problem of computing the exact characteristics of any subsegment of a Digital Straight Line (DSL) with known characteristics (a slope a/b, a shift to origin μ). We present here two new algorithms that solve this problem, whose correctnesses are fully proved. Their principle is to descend/climb the Stern-Brocot tree of fractions in a topdown/bottom-up way. The top-down algorithm SmartDSS has a time complexity which depends on the sum of the quotients of the continued fraction of the output slope and on the number of pattern repetitions. As a corollary, its time complexity is bounded by the sum of the quotients of the continued fraction of the input slope, Said and Lachaud (2009) [18]. The bottom-up algorithm ReversedSmartDSS has a time complexity proportional to the difference of depth of the input slope and the slope of the output segment, Said and Lachaud (2011) [17]. As a corollary, its complexity is thus logarithmic in the coefficients of the input slope. These algorithms are also efficient in practice, as shown by a series of experiments comparing these new algorithms with standard arithmetic digital straight segment recognition.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.