StableProxies
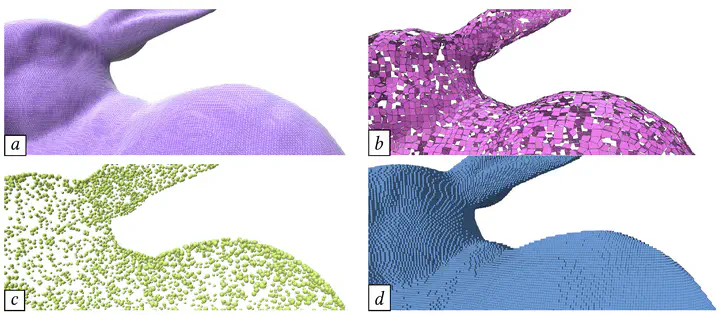 Heterogenous data
Heterogenous dataStart date: Feb. 2023
The objective of the project is to propose new calculus models for the geometry processing of large, heterogeneous and complex geometrical objects. The targeted geometrical models (polygonal meshes, point clouds, surfaces of voxel sets) are usually defective for direct geometry processing: deficient or missing topology, self-intersections, holes, non-manifold parts, perturbations, outliers. Their common characteristic is to be approximations of an underlying smooth object and not an interpolation of its boundary. Our approach is to build stable geometric proxies (embedded in a regular lattice) for these various data, for two main goals: first to guarantee that the estimates or the results of the calculus are theoretically accurate or stable (when compared to their counterpart from the continuous analysis), second to design practical algorithms that scale well in terms of performance, numerical stability, capability to represent various dimensional objects (volumes, surfaces, 1d curves in space), and memory efficiency (thanks to a multiscale approach). This unified approach provides generic tools to measure quantities and perform calculus on such discrete data, and allows modeling and simulation of complex and natural phenomena on various real geometric data. We will more specifically explore applications in material engineering (analysis and calculus on high resolution volumetric surfaces from micro-tomographic images, fracture simulation on materials…), the geometry processing of acquired massive, highly detailed, 3D point clouds (e.g, billions of points acquired with LiDAR or photogrammetry).



