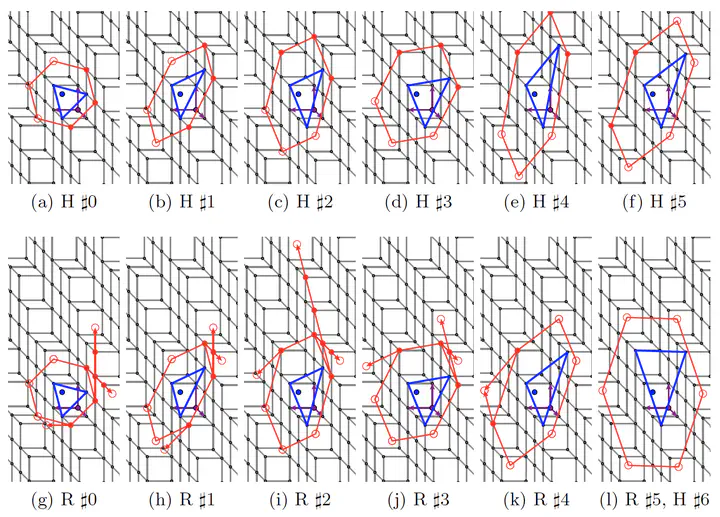
Abstract
We present a new plane-probing algorithm, i.e., an algorithm that computes the normal vector of a digital plane from a starting point and a predicate “Is a point x in the digital plane?”. This predicate is used to probe the digital plane as locally as possible and decide on-the-fly the next points to consider. We show that this algorithm returns the same vector as another plane-probing algorithm proposed in Lachaud et al. (J. Math. Imaging Vis., 59(1): 23-39, 2017), but requires fewer probes. The theoretical upper bound is indeed lowered from $O(\omega \log \omega)$ to $O(\omega )$ calls to the predicate, where $\omega $ is the arithmetical thickness of the digital plane, and far fewer calls are experimentally observed on average. This reduction is made possible by a study that shows how to avoid computations that do not contribute to the final solution. In the context of digital surface analysis, this new algorithm is expected to be of great interest for normal estimation and shape reconstruction.
Jacques-Olivier Lachaud
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.