Dynamic Minimum Length Polygon

Abstract

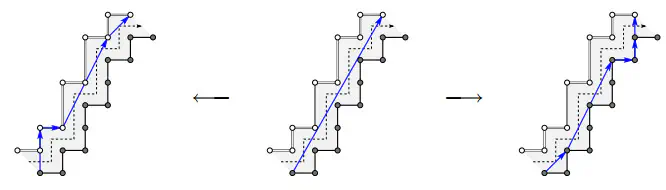
This paper presents a formal framework for representing all reversible polygonalizations of a digital contour (i.e. the boundary of a digital object). Within these polygonal approximations, a set of local operations is defined with given properties, e.g., decreasing the total length of the polygon or diminishing the number of quadrant changes. We show that, whatever the starting reversible polygonal approximation, iterating these operations leads to a specific polygon: the Minimum Length Polygon. This object is thus the natural representative for the whole class of reversible polygonal approximations of a digital contour. Since all presented operations are local, we obtain the first dynamic algorithm for computing the MLP. This gives us a sublinear time algorithm for computing the MLP of a contour, when the MLP of a slightly different contour is known.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.