Lightweight Curvature Estimation on Point Clouds with Randomized Corrected Curvature Measures

Abstract

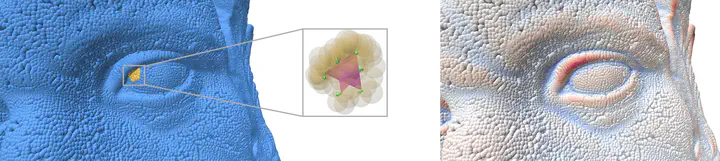
The estimation of differential quantities on oriented point cloud is a classical step for many geometry processing tasks in computer graphics and vision. Even if many solutions exist to estimate such quantities, they usually fail at satisfying both a stable estimation with theoretical guarantee, and the efficiency of the associated algorithm. Relying on the notion of corrected curvature measures [LRT22, LRTC20] designed for surfaces, the method introduced in this paper meets both requirements. Given a point of interest and a few nearest neighbours, our method estimates the whole curvature tensor information by generating random triangles within these neighbours and normalising the corrected curvature measures by the corrected area measure. We provide a stability theorem showing that our pointwise curvatures are accurate and convergent, provided the noise in position and normal information has a variance smaller than the radius of neighbourhood. Experiments and comparisons with the state-of-the-art confirm that our approach is more accurate and much faster than alternatives. The method is fully parallelizable, requires only one nearest neighbour request per point of computation, and is trivial to implement.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.