Abstract
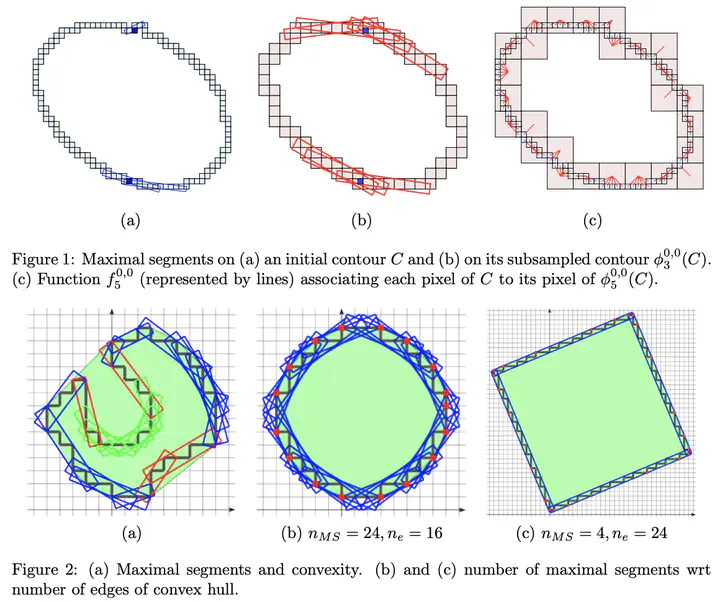
It is often interesting to study the geometry of digitization of euclidean shapes in the plane, and to establish connections between the discrete geometry computed along the digital contour and the euclidean geometry of the initial shape. this task is essential in image analysis, where the initial euclidean shape has been lost through various acquisition and segmentation processes. Maximal segments are the connected pieces of digital straight lines that are contained in the digital contour and that are not extensible (if they are extended on either side, the formed set is no more a digital straight segment). Maximal segments appear to hold many interesting properties for analyzing digital shapes. We will show here that they provide good length and tangent estimators and also characterize the convex and concave parts of the shape. They induce discrete geometric estimators that are multigrid convergent, with a quantifiable error. These asymptotic properties of maximal segments are also extremely useful to detect the local meaningful scales at which the shape should be analyzed: in this sense, they provide an unsupervised method to determine locally the level of noise that is damaging the shape. Finally, although the presented tool is 2D, we will show that it can nevertheless be used to some extent for 3D shape analysis.
Jacques-Olivier Lachaud
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.