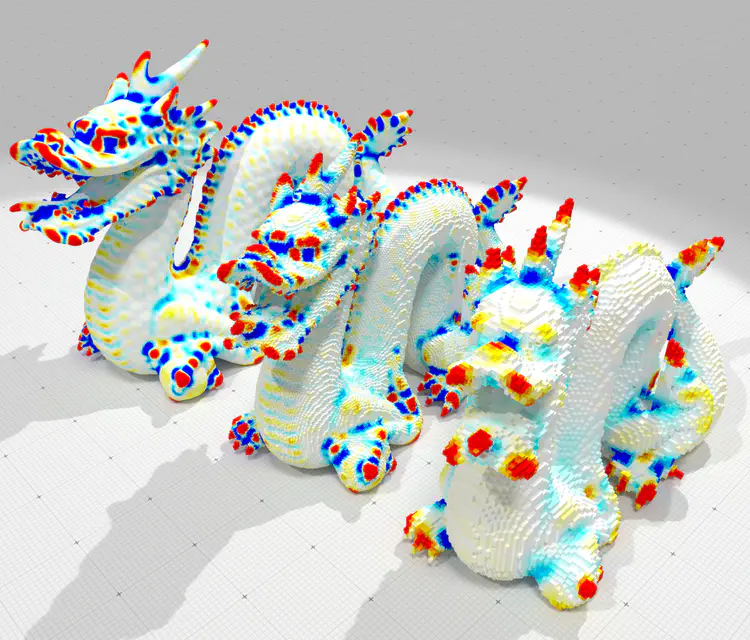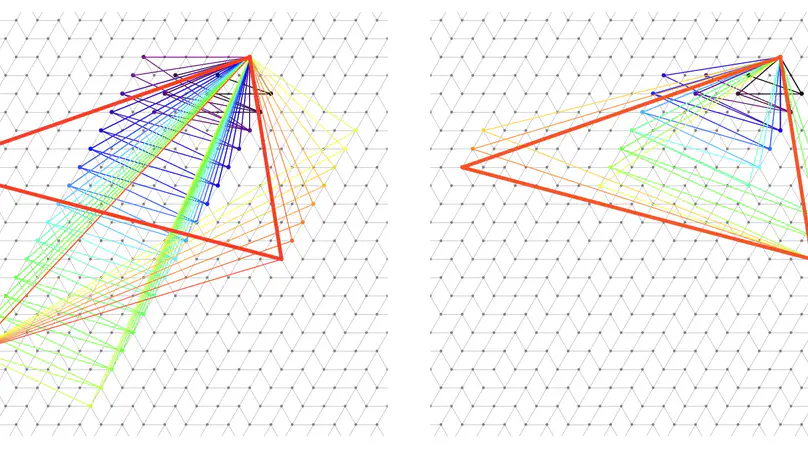
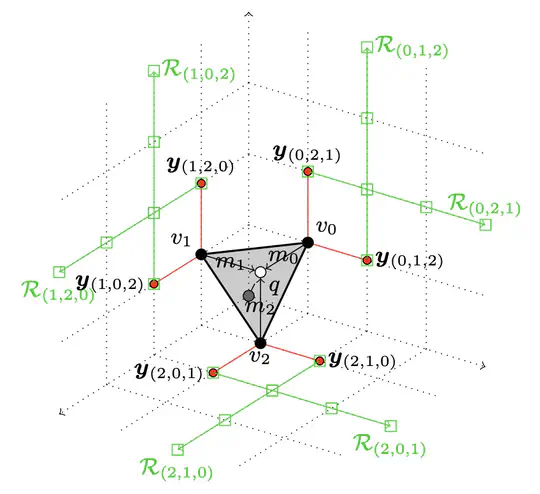
When processing the geometry of digital surfaces (boundaries of voxel sets), linear local structures such as pieces of digital planes play an important role. To capture such geometrical features, plane-probing algorithms have demonstrated their strength: starting from an initial triangle, the digital structure is locally probed to expand the triangle approximating the plane parameters more and more precisely (converging to the exact parameters for infinite digital planes). Among the different plane-probing algorithms, the L-algorithm is a plane-probing algorithm variant which takes into account a generally larger neighborhood of points for its update process. We show in this paper that this algorithm has the advantage to guarantee the so-called Delaunay property of the set of probing points, which has interesting consequences: it provides a minimal basis of the plane and guarantees an as-local-as-possible computation.

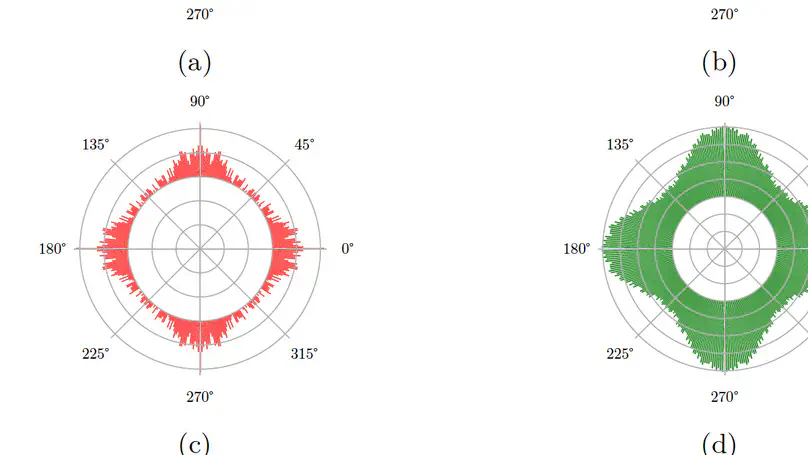
Preserving surfaces or volumes of digital objects is crucial when applying transformations of 2D/3D digital objects in medical images and computer vision. To achieve this goal, the digital geometry community has focused on characterizing bijective digitized rotations and reflections. However, the angular distribution of these bijective rigid transformations is far from being dense. Other bijective approximations of rigid transformations have been proposed, but the state-of-the-art methods lack the experimental evaluations necessary to include them in real-life applications. This paper presents several new methods to approximate digitized rotations with bijective transformations, including the composition of bijective digitized reflections, bijective rotation by circles and bijective rotation through optimal transport. These new methods and several classical ones are compared both in terms of accuracy with respect to Euclidean rotations, and in terms of computational complexity and practical speed in real-time applications.

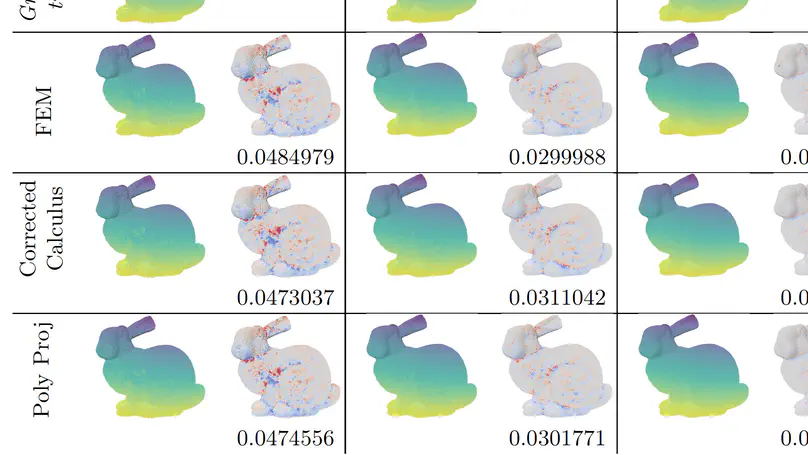
Defining consistent calculus frameworks on discrete meshes is useful for processing the geometry of meshes or model numerical simulations and variational problems onto them. However digital surfaces (boundary of voxels) cannot benefit directly from the classical mesh calculus frameworks, since their vertex and face geometry is too poor to capture the geometry of the underlying smooth Euclidean surface well enough. This paper proposes two new calculus frameworks dedicated to digital surfaces, which exploit a corrected normal field, in a manner similar to the recent digital calculus of [3]. First we build a corrected interpolated calculus by defining inner products with position and normal interpolation in the Grassmannian. Second we present a corrected finite element method which adapts the standard Finite Element Method with a corrected metric per element. Experiments show that these digital calculus frameworks seem to converge toward the continuous calculus, offer a valid alternative to classical mesh calculus, and induce effective tools for digital surface processing tasks.

Full convexity has been recently proposed as an alternative definition of digital convexity. In contrast to classical definitions, fully convex sets are always connected and even simply connected whatever the dimension, while remaining digitally convex in the usual sense. Several characterizations were proposed in former works, either based on lattice intersection enumeration with several convex hulls, or using the idempotence of an envelope operator. We continue these efforts by studying simple properties of real convex sets whose digital counterparts remain largely misunderstood. First we study if we can define full convexity through variants of the usual continuous convexity via segments inclusion, i.e. ``for all pair of points of X, the straight segment joining them must lie within the set X’. We show an equivalence of full convexity with this segment convexity in dimension 2, and counterexamples starting from dimension 3. If we consider now d-simplices instead of a segment (2-simplex), we achieve an equivalence in arbitrary dimension d. Secondly, we exhibit another characterization of full convexity, which is recursive with respect to the dimension and uses simple axis projections. This latter characterization leads to two immediate applications: a proof that digital balls are indeed fully convex, and a natural progressive measure of full convexity for arbitrary digital sets.

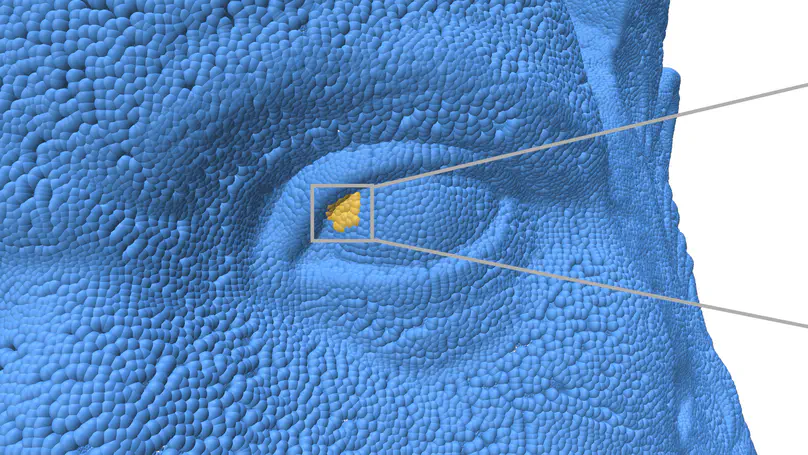
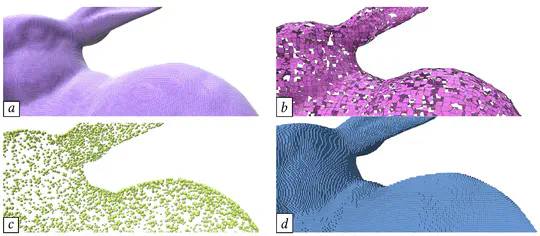
The estimation of differential quantities on oriented point cloud is a classical step for many geometry processing tasks in computer graphics and vision. Even if many solutions exist to estimate such quantities, they usually fail at satisfying both a stable estimation with theoretical guarantee, and the efficiency of the associated algorithm. Relying on the notion of corrected curvature measures [LRT22, LRTC20] designed for surfaces, the method introduced in this paper meets both requirements. Given a point of interest and a few nearest neighbours, our method estimates the whole curvature tensor information by generating random triangles within these neighbours and normalising the corrected curvature measures by the corrected area measure. We provide a stability theorem showing that our pointwise curvatures are accurate and convergent, provided the noise in position and normal information has a variance smaller than the radius of neighbourhood. Experiments and comparisons with the state-of-the-art confirm that our approach is more accurate and much faster than alternatives. The method is fully parallelizable, requires only one nearest neighbour request per point of computation, and is trivial to implement.

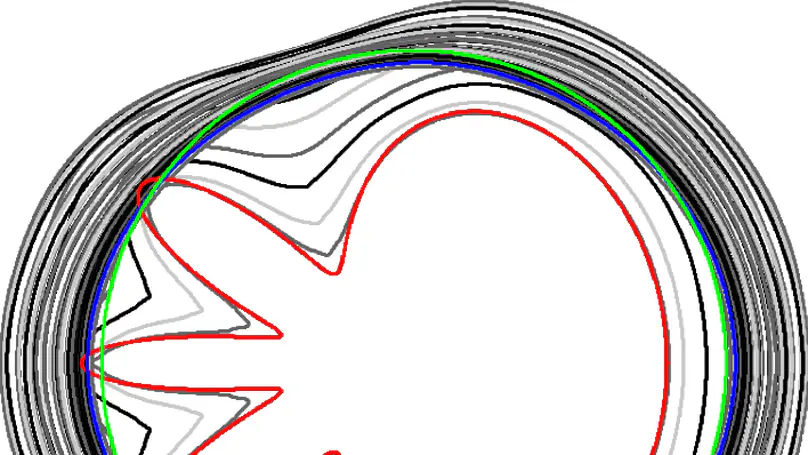
We propose a graph cut model to optimize bidimensional shapes with respect to the elastica energy. At each iteration our model selects the shape of minimum elastica value among a set of candidates generated by a discrete process that we call the balance coefficient flow. In this work we show how the balance coefficient flow relates with the curve-shortening flow and how our model can be included in an image segmentation pipeline. Finally, we provide a study to evaluate the effects of our model in the image segmentation task.

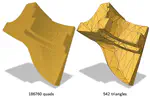
This paper proposes full convexity as an alternative definition of digital convexity, which is valid in arbitrary dimension. It solves many problems related to its usual definitions, like possible non connectedness or non simple connectedness, while encompassing its desirable features. Fully convex sets are digitally convex, but are also connected and simply connected. They have a morphological characterisation, which induces a simple convexity test algorithm. Arithmetic planes are fully convex too. Full convexity implies local full convexity, hence it enables local shape analysis, with an unambiguous definition of convex, concave and planar points. As a kind of relative full convexity, we propose a natural definition of tangent subsets to a digital set. It gives rise to the tangential cover in 2D, and to consistent extensions in arbitrary dimension. Finally we present two applications of tangency: the first one is a simple algorithm for building a polygonal mesh from a set of digital points, with reversibility property, the second one is the definition and computation of shortest paths within digital sets.