Analytical description of digital intersections: Minimal parameters and multiscale representation
Abstract
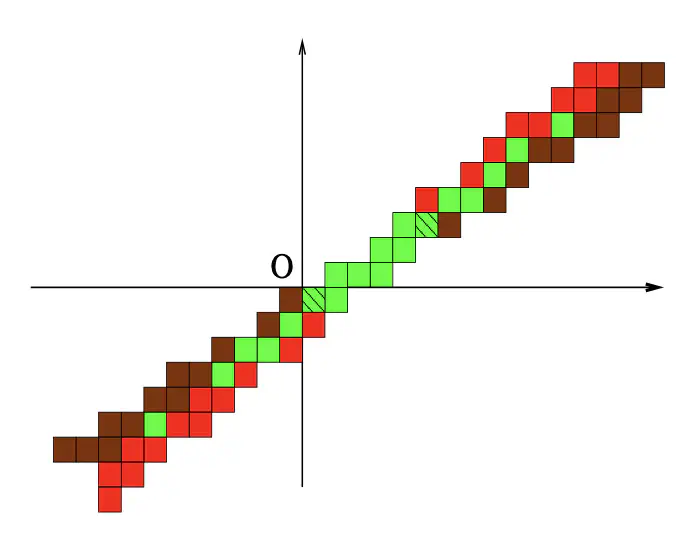
The paper contributes to a multiscale theory of digital shapes by presenting novel methods for a multiscale representation of digital lines and their intersections according to the Stern-Brocot tree. We give a new definition of the intersection (main conntected part) of two specific digital straight lines on the same quadrant (First quadrant). More precisely, we give some new results about the minimal set of parameters (i.e. slope (a,b), shift (µ), parity (even or odd), and the coordinates of the upper leaning points) for each line and their intersections.
Type
Publication
Theoretical Computer Science, 784: 99-112, 2019
Digital Geometry
Digital Straightness
2D
Multiscale Geometry
Stern-Brocot Tree
Digital Straight Segment Recognition
Authors
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.