Constructing Iso-Surfaces Satisfying the Delaunay Constraint; Application to the Skeleton Computation
Abstract
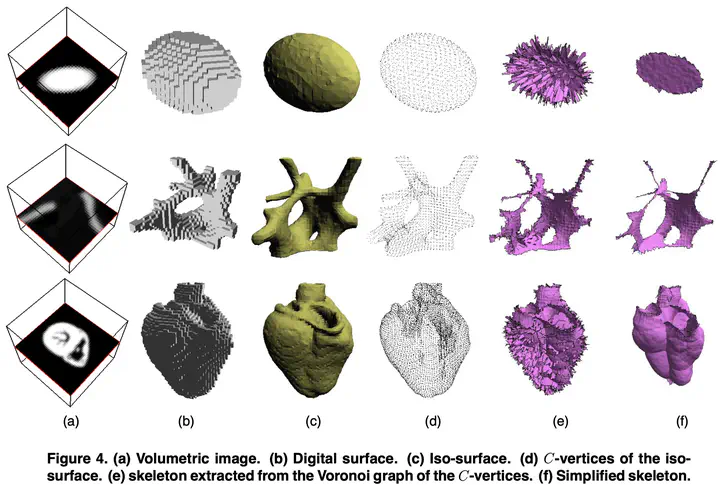
We design a new model for an image iso-surface which lies in the Delaunay graph of its vertices. Within each 8-cube of the image, a set of loops is computed according to the connectedness chosen for inner and outer voxels. Next, a triangulation is computed which respects the local geometry of these loops. Efficiency is obtained through the use of a look-up table which summarizes the algebraic tests that are required of each case. The inclusion of the iso-surface in the Delaunay triangulation has significant consequences. We derive a volume representation of the object, along with its skeleton. An example depicts the complete construction of our iso-surface, volume representation and skeleton computation.
Type
Publication
Proc. 10th Int. Conf. on Image Analysis and Processing (ICIAP'99), Venice, Italy, Sept. 27-29, pp 382-387, 1999. IEEE
Digital Topology
Isosurface Extraction
Marching Cubes
Delaunay Triangulation
Skeleton
3D
Geometry Processing
Authors
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.