Digital Calculus Frameworks and Comparative Evaluation of Their Laplace-Beltrami Operators

Abstract

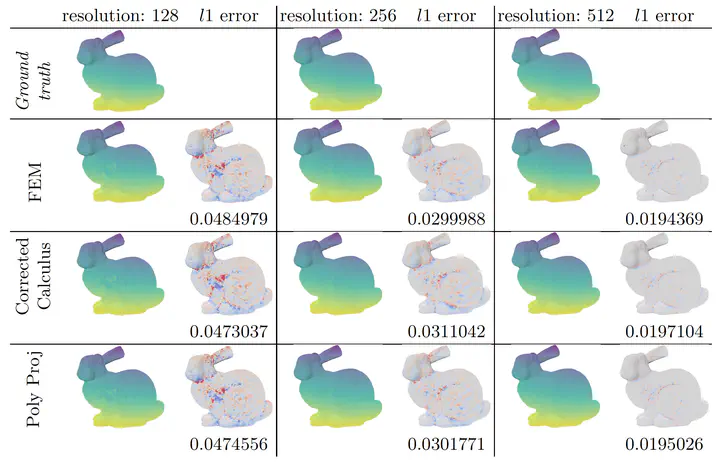
Defining consistent calculus frameworks on discrete meshes is useful for processing the geometry of meshes or model numerical simulations and variational problems onto them. However digital surfaces (boundary of voxels) cannot benefit directly from the classical mesh calculus frameworks, since their vertex and face geometry is too poor to capture the geometry of the underlying smooth Euclidean surface well enough. This paper proposes two new calculus frameworks dedicated to digital surfaces, which exploit a corrected normal field, in a manner similar to the recent digital calculus of [3]. First we build a corrected interpolated calculus by defining inner products with position and normal interpolation in the Grassmannian. Second we present a corrected finite element method which adapts the standard Finite Element Method with a corrected metric per element. Experiments show that these digital calculus frameworks seem to converge toward the continuous calculus, offer a valid alternative to classical mesh calculus, and induce effective tools for digital surface processing tasks.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.