Abstract
Preserving surfaces or volumes of digital objects is crucial when applying transformations of 2D/3D digital objects in medical images and computer vision. To achieve this goal, the digital geometry community has focused on characterizing bijective digitized rotations and reflections. However, the angular distribution of these bijective rigid transformations is far from being dense. Other bijective approximations of rigid transformations have been proposed, but the state-of-the-art methods lack the experimental evaluations necessary to include them in real-life applications. This paper presents several new methods to approximate digitized rotations with bijective transformations, including the composition of bijective digitized reflections, bijective rotation by circles and bijective rotation through optimal transport. These new methods and several classical ones are compared both in terms of accuracy with respect to Euclidean rotations, and in terms of computational complexity and practical speed in real-time applications.
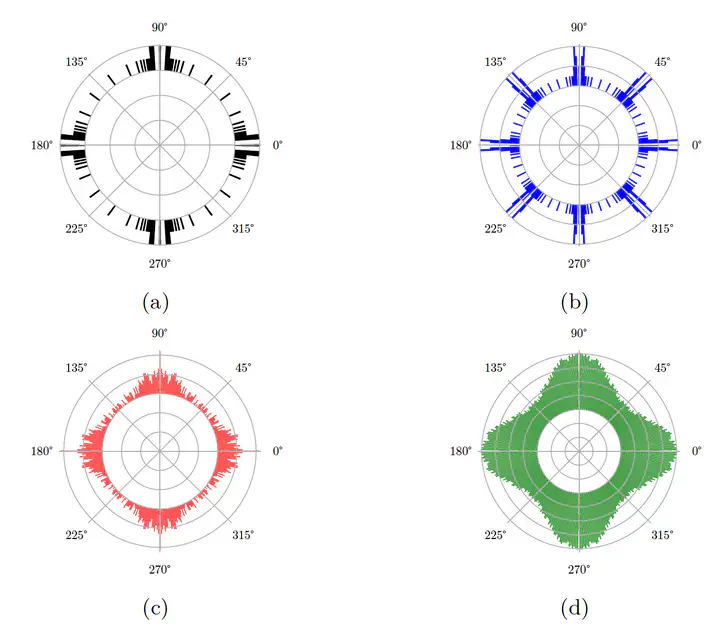
Visual comparison of a few bjective rotations in Z2
The bigger the radius, the closer the digital rotations are close to the continuous rotations.
| Bijective rotation along circles (RBC) | Bijective rotation along rings of radius 2 and optimal transport (OTC2) |
 |  |
| Bijective rotation along rings of radius 3 and optimal transport (OTC3) | Bijective rotation along rings of radius 4 and optimal transport (OTC4) |
 |  |
Jacques-Olivier Lachaud
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.