Géométrie discréte et images numériques
Abstract
La topologie digitale est l’étude des propriétés des objets discrets qui sont indépendantes de leurs propriétés métriques. L’existence d’un trou dans un objet (au sens où un anneau a un trou et un pantalon a deux trous) n’est pas modifiée par une déformation ``continue’’ de l’objet. D’un point de vue algorithmique, on cherche souvent à concevoir des méthodes de traitement d’image qui ne modifient pas la topologie des objets (connexité, existence d’un trou, etc). Le formalisme mathématique nécessaire pour définir de telles méthodes est assez abstrait.
Au sens de la topologie, on peut dire que toutes les courbes fermées simples sont équivalentes (ou homéomorphes), et toute courbe fermée simple dans le plan possède un trou, au sens où elle sépare le plan (théorème de Jordan). La notion de déformation continue est formalisée dans la notion d’homotopie. Cette notion permet d’associer aux objets discrets des objets algébriques (des groupes), de manière qu’à deux objets topologiquement équivalents soient associés deux groupes équivalents. Ces invariants algébriques sont fondamentaux dans l’étude des propriétés topologiques des objets. Cette même notion d’homotopie permet de définir les points simples, qui sont les points qu’on peut enlever d’un objet sans en modifier la topologie. Les points simples sont en particulier à la base des algorithmes de squelettisation topologique.
D’autres notions fondamentales en topologie sont les frontières et les surfaces. Par exemple, la frontière d’un objet connexe sans cavité est connexe. Une telle frontière doit satisfaire la propriété de séparation de Jordan. En topologie digitale, on se donne les outils pour définir des frontières et surfaces discrètes qui ont une bonne propriété de séparation. Ces frontières sont ensuite munies de structures de graphes, qui permettent de les construire et de les parcourir efficacement. Des outils existent ensuite pour estimer la géométrie de ces objets ou pour en fabriquer des modèles géométriques.
Type
Publication
Géométrie discréte et images numériques, 3 - Topologie, courbes et surfaces discrètes, Hermès, 2007
Digital Topology
Digital Surface
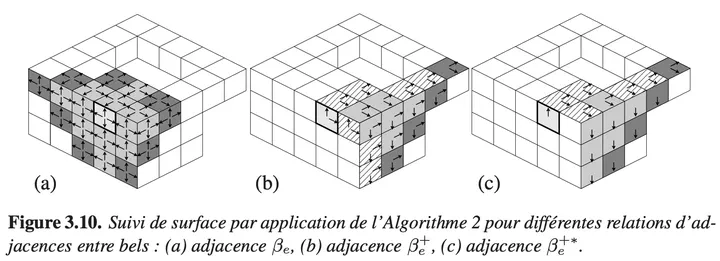
Digital Surface Tracking
Jordan Pairs
Digital Homotopy
Jordan Theorem
Curve Index
ND
Authors
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.