Computing the Characteristics of a SubSegment of a Digital Straight Line in Logarithmic Time

M. Said, Jacques-Olivier Lachaud
April, 2011
PDF Cite Project Code (DGtal)

Abstract

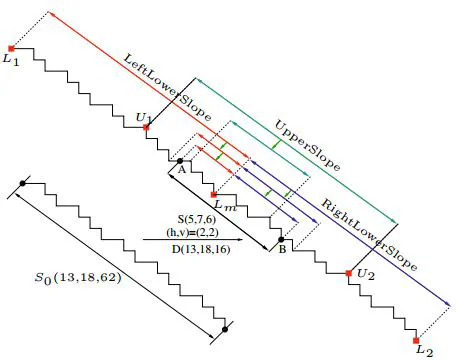
We address the problem of computing the exact characteristics of any subsegment of a digital straight line with known characteristics. We present a new algorithm that solves this problem, whose correctness is proved. Its principle is to climb the Stern-Brocot tree of fraction in a bottom-up way. Its worst-time complexity is proportionnal to the difference of depth of the slope of the input line and the slope of the output segment. It is thus logarithmic in the coefficients of the input slope. We have tested the effectiveness of this algorithm by computing a multiscale representation of a digital shape, based only on a digital straight segment decomposition of its boundary.

Type
Conference paper
Publication
Proc. International Conference on Discrete Geometry for Computer Imagery (DGCI2011), volume 6607 of Lecture Notes in Computer Science, pp 320-332, 2011. Springer, Cham
discrete geometry digital straight segment recognition digital straightness 2D Christoffel word pattern continued fraction digital geometry
Jacques-Olivier Lachaud
Jacques-Olivier Lachaud
Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.