Phase-field modelling and computing for a large number of phases

Abstract

We propose a framework to represent a partition that evolves under mean curvature flows and volume constraints. Its principle follows a phase-field representation for each region of the partition, as well as classical Allen-Cahn equations for its evolution. We focus on the evolution and on the optimization of problems involving high resolution data with many regions in the partition. In this context, standard phase-field approaches require a lot of memory (one image per region) and computation timings increase at least as fast as the number of regions. We propose a more efficient storage strategy with a dedicated multi-image representation that retains only significant phase field values at each discretization point. We show that this strategy alone is unfortunately inefficient with classical phase field models. This is due to non local terms and low convergence rate. We therefore introduce and analyze an improved phase field model that localizes each phase field around its associated region, and which fully benefits of our storage strategy. 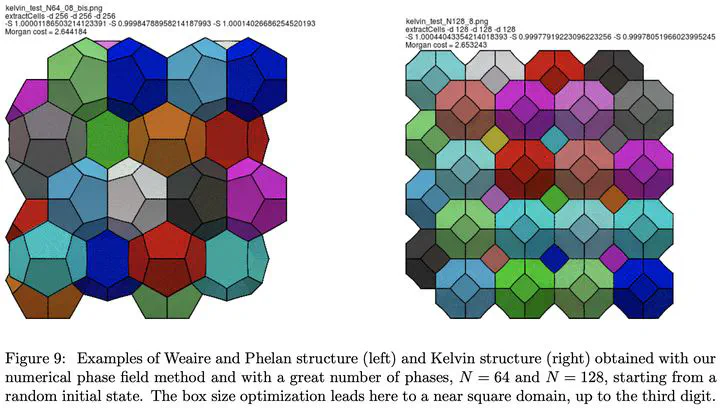To demonstrate the efficiency of the new multiphase field framework, we apply it to the famous 3D honeycomb problem and the conjecture of Weaire-Phelan’s tiling.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.