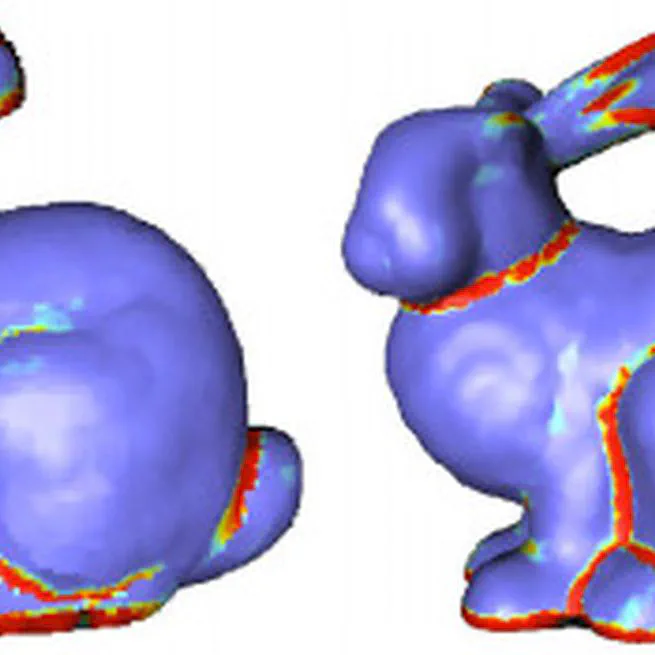
Voronoi-Based Geometry Estimator for 3D Digital Surfaces
Jan 1, 2014
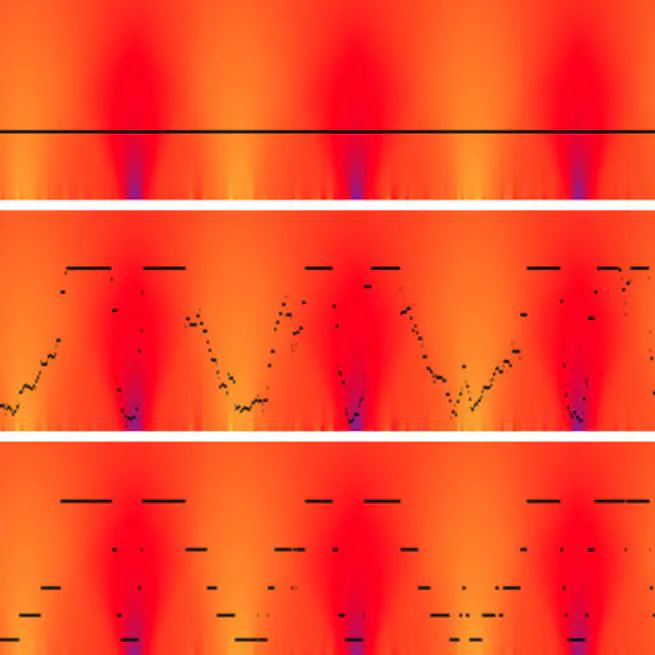
Parameter-Free and Multigrid Convergent Digital Curvature Estimators
Jan 1, 2014
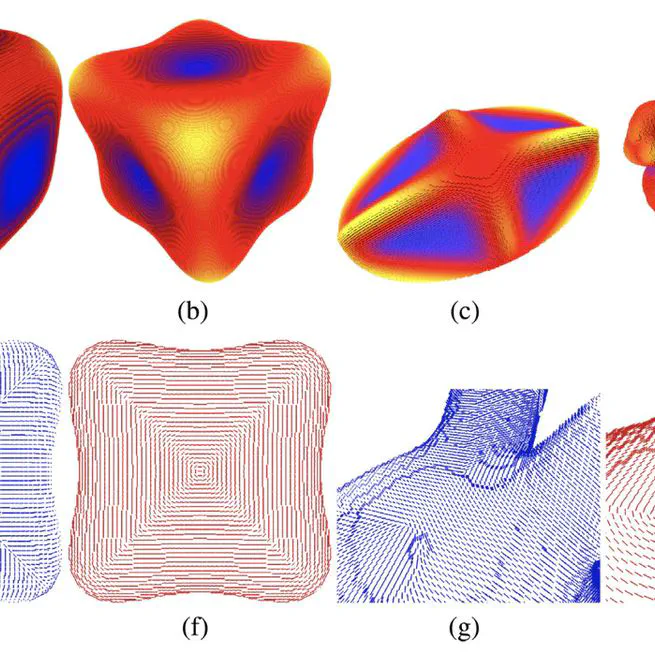
Multigrid convergent principal curvature estimators in digital geometry
Jan 1, 2014

Multigrid convergence of digital curvature estimators
Invited talk.
Nov 18, 2013
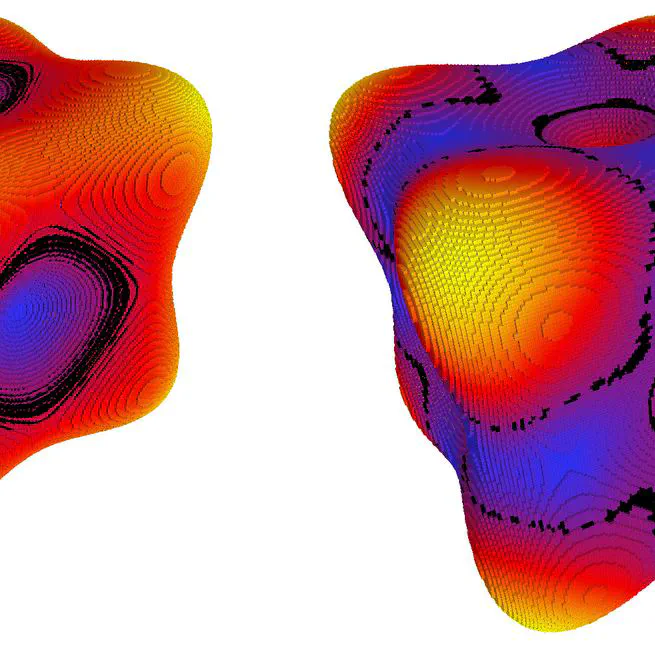
Integral based Curvature Estimators in Digital Geometry
Jan 1, 2013
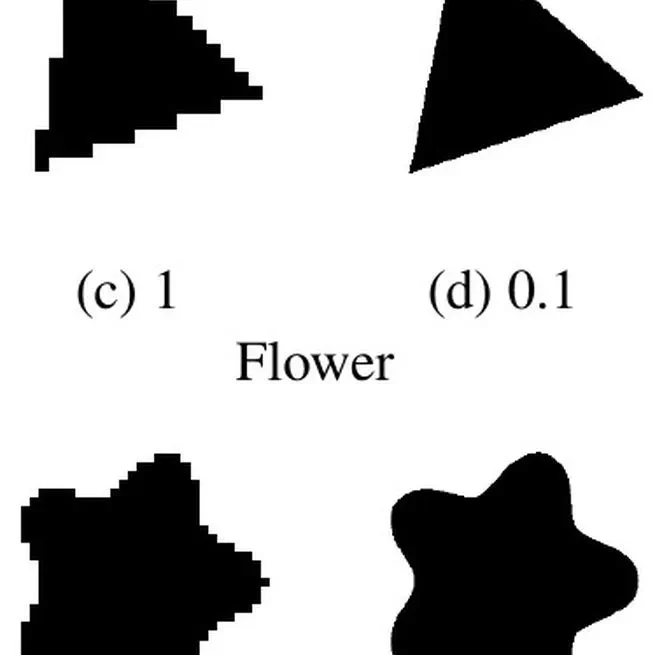
Multigrid Convergence of Discrete Geometric Estimators
Jan 1, 2012
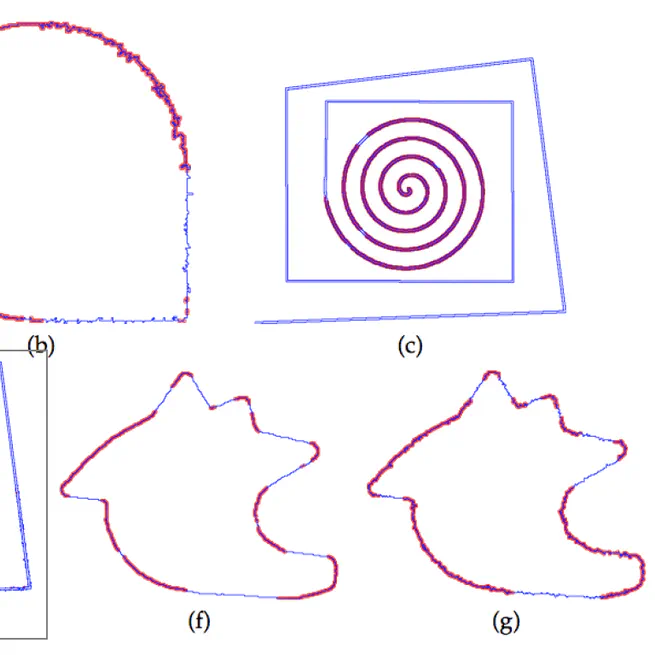
Asymptotic linear digital geometry and applications
Invited talk.
Feb 8, 2011
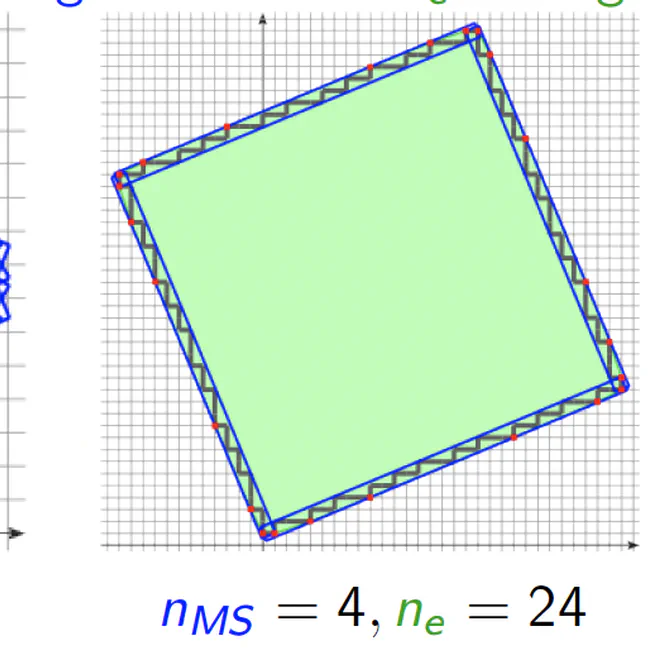
Asymptotic linear digital geometry
Invited talk.
Feb 8, 2011
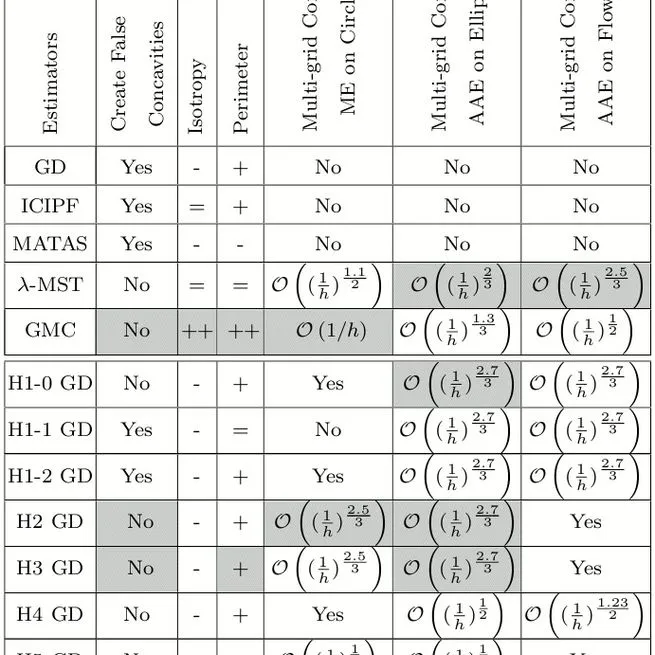
Comparison and improvement of tangent estimators on digital curves
Aug 1, 2009
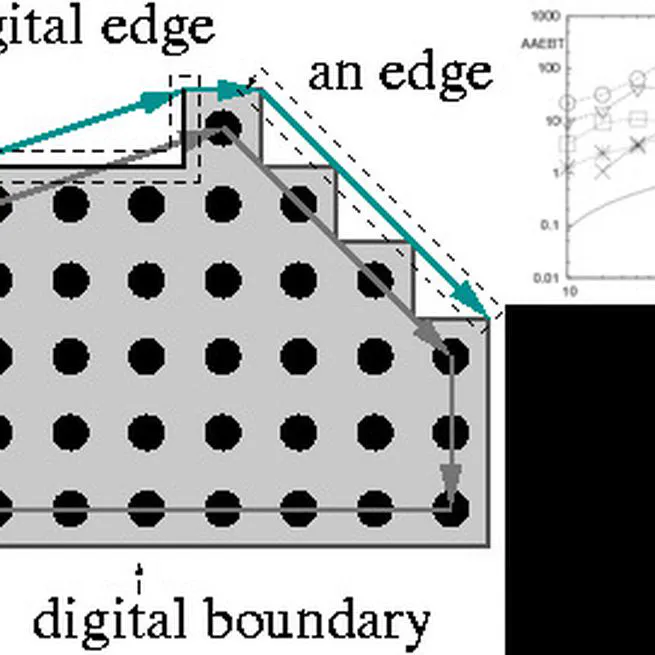
Experimental Comparison of Continuous and Discrete Tangent Estimators Along Digital Curves
Mar 1, 2008