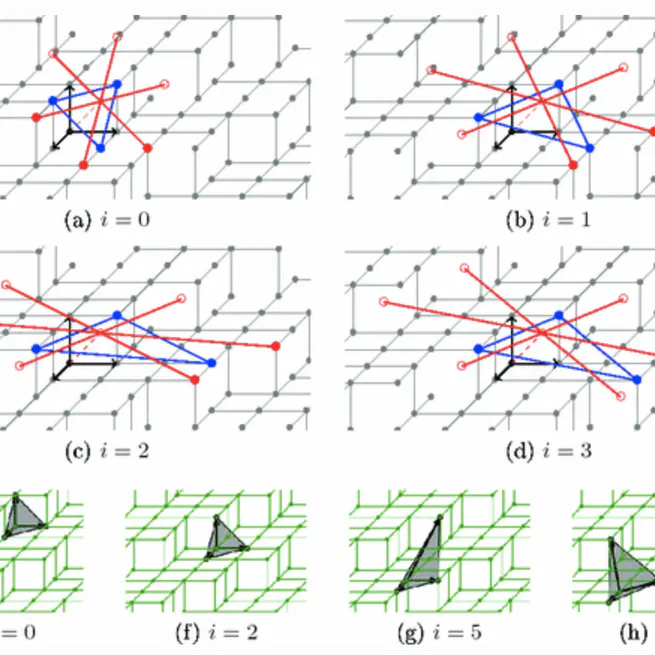
Computation of the Normal Vector to a Digital Plane by Sampling Significant Points
Jan 1, 2016
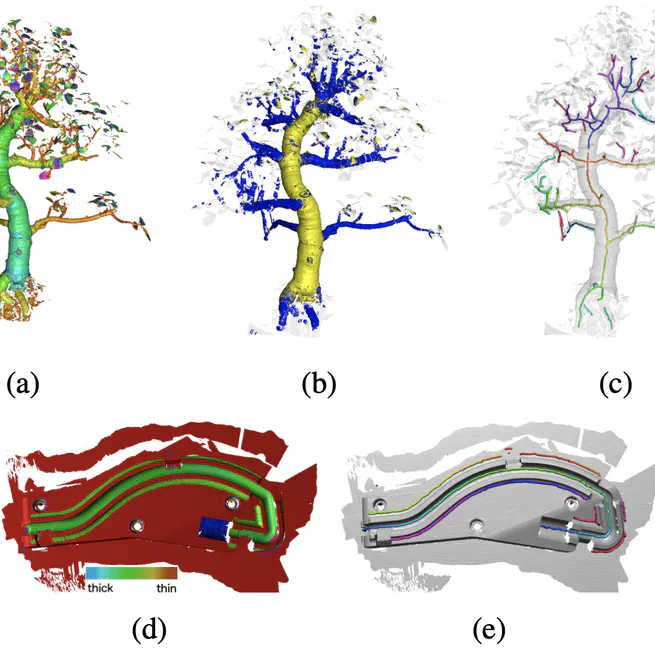
Centerline detection on partial mesh scans by confidence vote in accumulation map
Jan 1, 2016
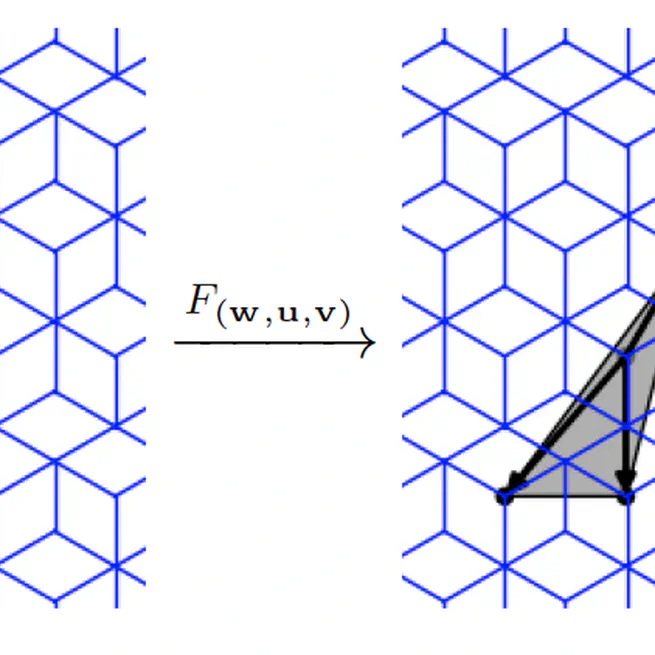
An output-sensitive algorithm to compute the normal vector of a digital plane
Jan 1, 2016

Cross Border Meeting on Discrete and Computational Geometry and Applications
Organizer.
Nov 9, 2015

CoMeDiC
Convergent Metrics for Digital Calculus (ANR project ANR-15-CE40-0006) Oct. 2015 - Jul. 2021 / Principal Investigator
Oct 1, 2015

Precise Cross-Section Estimation on Tubular Organs
Jan 1, 2015
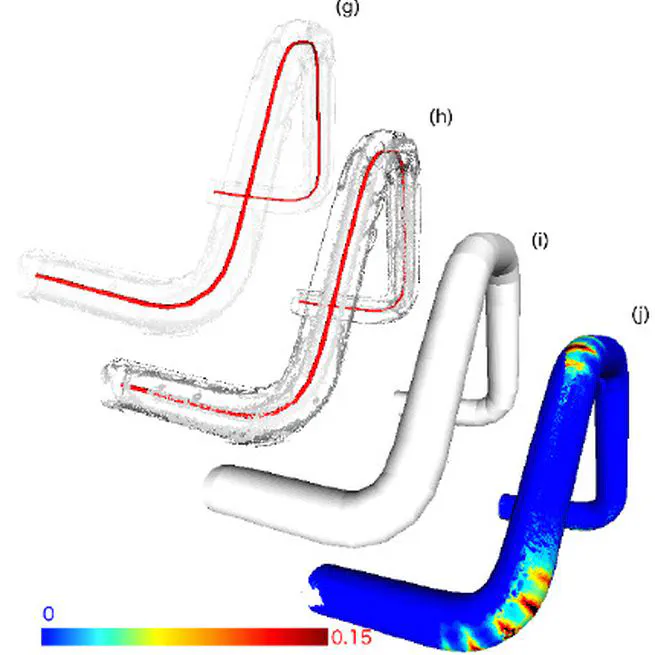
3D Geometric Analysis of Tubular Objects Based on Surface Normal Accumulation
Jan 1, 2015
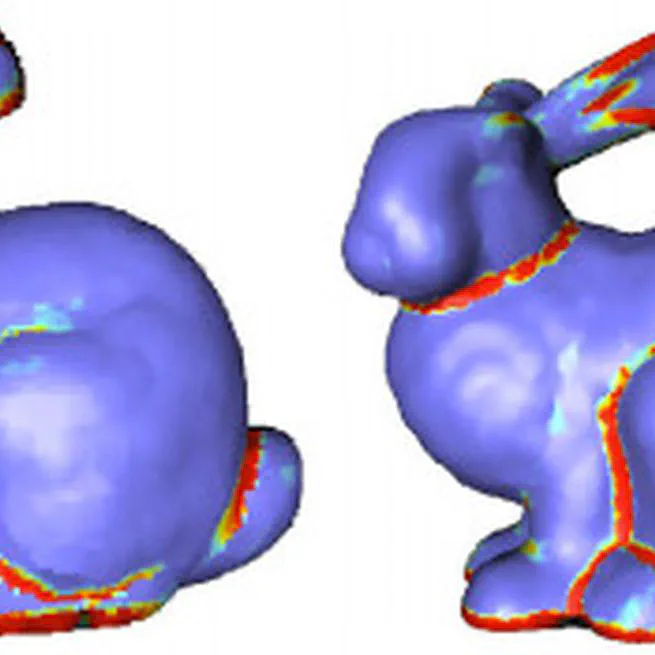
Voronoi-Based Geometry Estimator for 3D Digital Surfaces
Jan 1, 2014
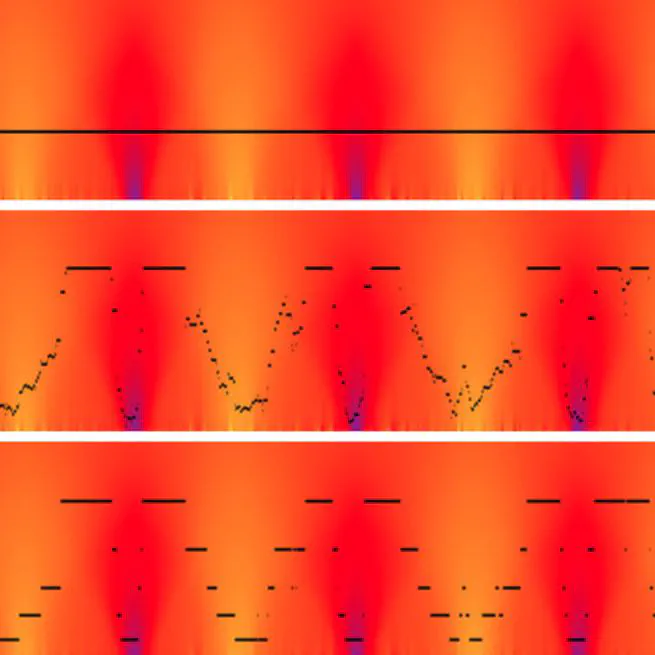
Parameter-Free and Multigrid Convergent Digital Curvature Estimators
Jan 1, 2014
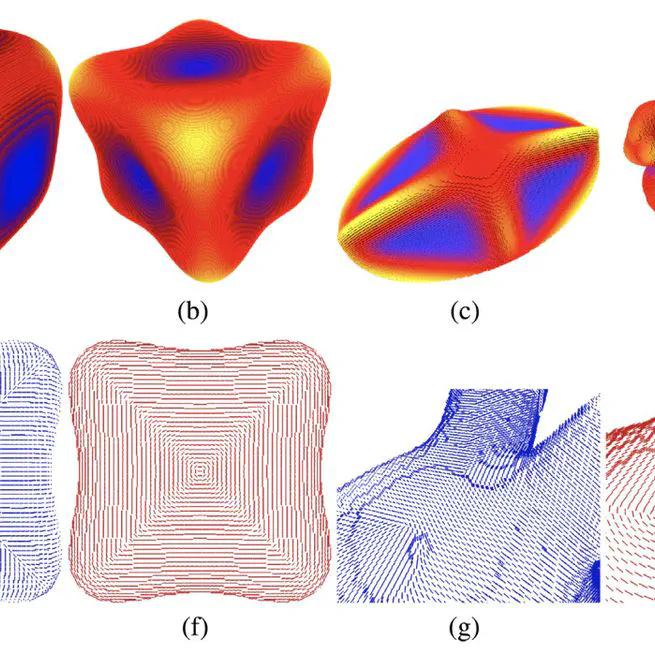
Multigrid convergent principal curvature estimators in digital geometry
Jan 1, 2014