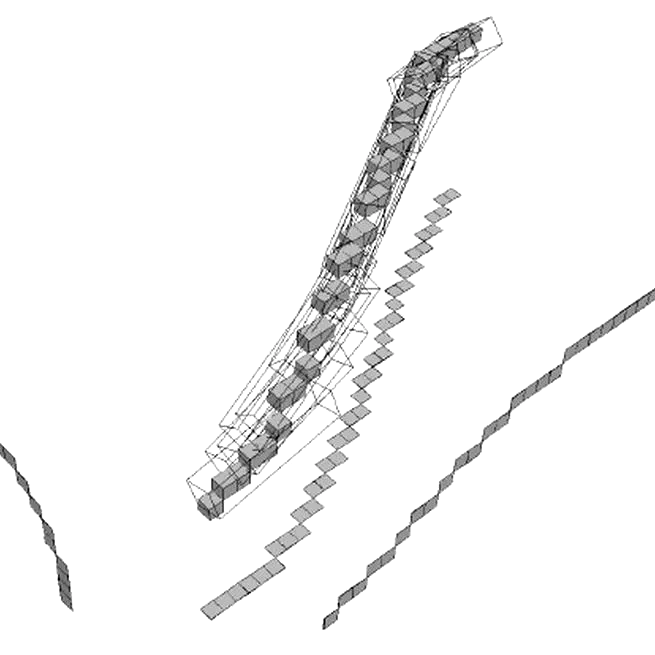
Tangent estimation along 3D digital curves
Nov 1, 2012
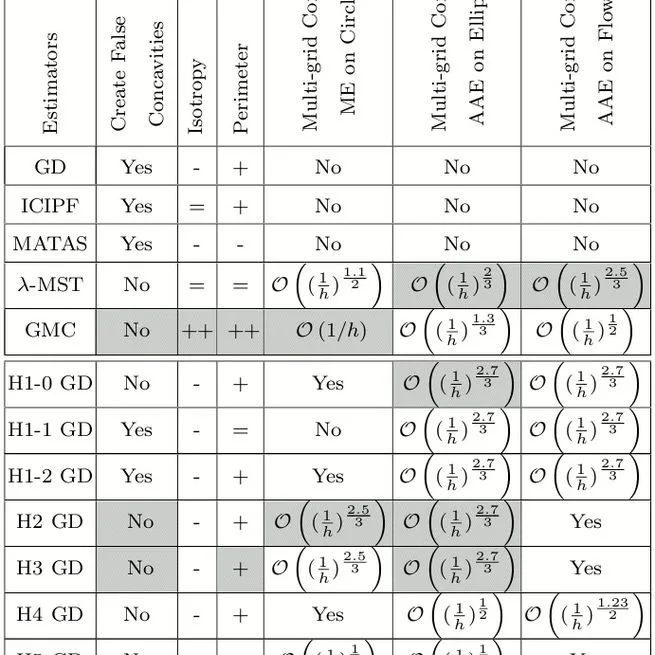
Comparison and improvement of tangent estimators on digital curves
Aug 1, 2009

Multi-Label Simple Points Definition for 3D Images Digital Deformable Model
Jan 1, 2009
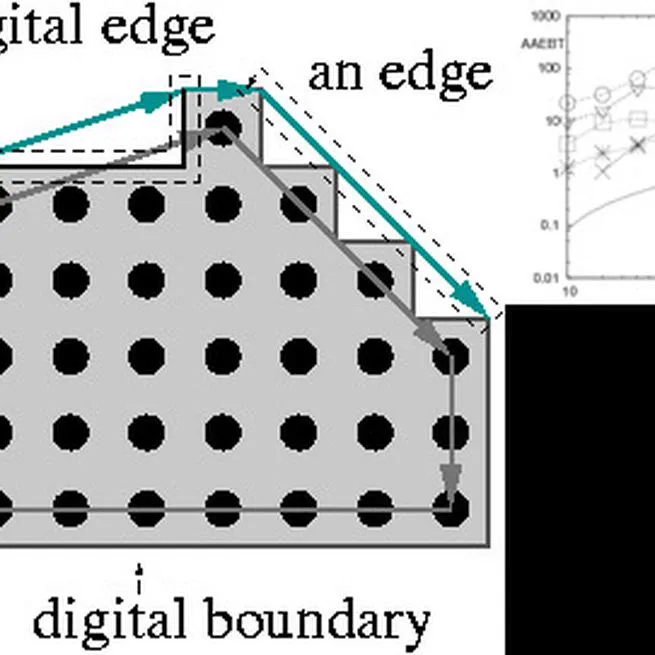
Experimental Comparison of Continuous and Discrete Tangent Estimators Along Digital Curves
Mar 1, 2008
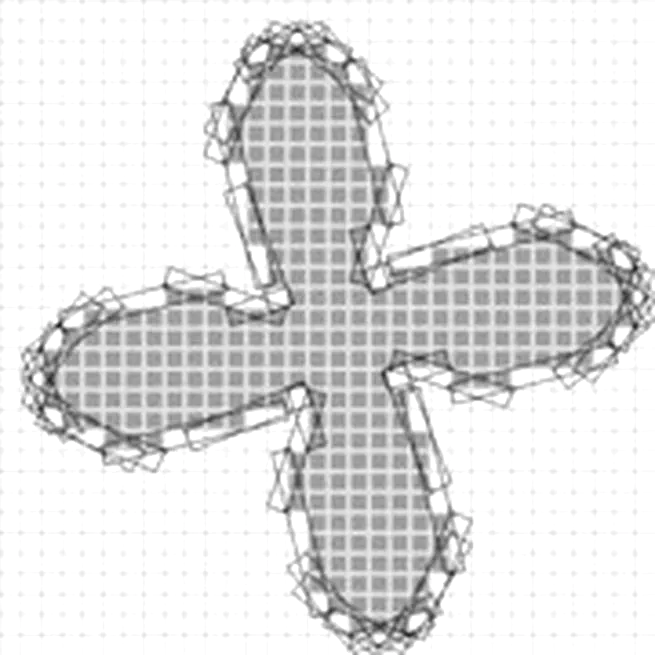
Fast, Accurate and Convergent Tangent Estimation on Digital Contours
Oct 1, 2007
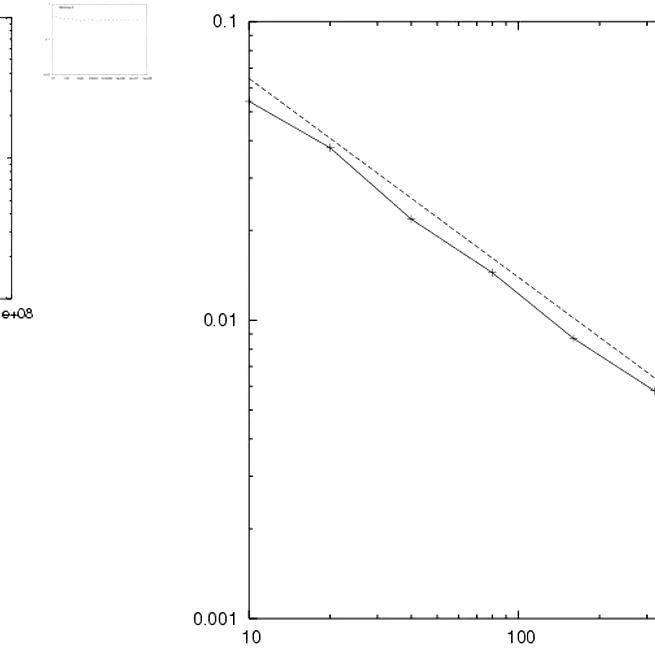
Convex shapes and convergence speed of discrete tangent estimators
Nov 1, 2006
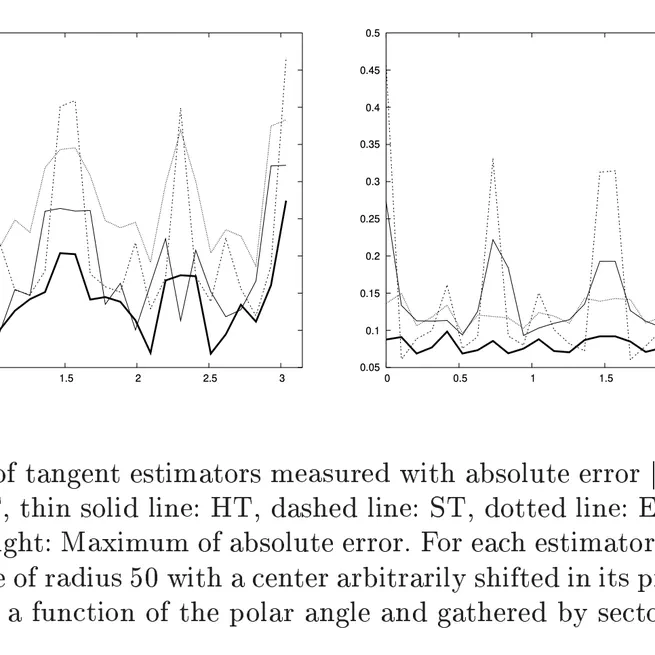
Analysis and comparative evaluation of discrete tangent estimators
Jan 1, 2005