
Robust and Convergent Curvature and Normal Estimators with Digital Integral Invariants
Jan 1, 2017
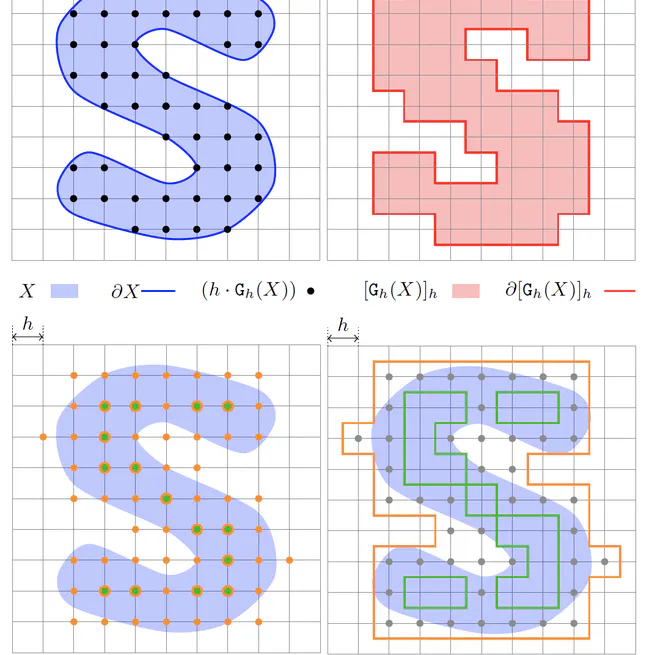
Convergent Geometric Estimators with Digital Volume and Surface Integrals
Keynote speaker at DGCI 2016, Nantes.
Apr 18, 2016
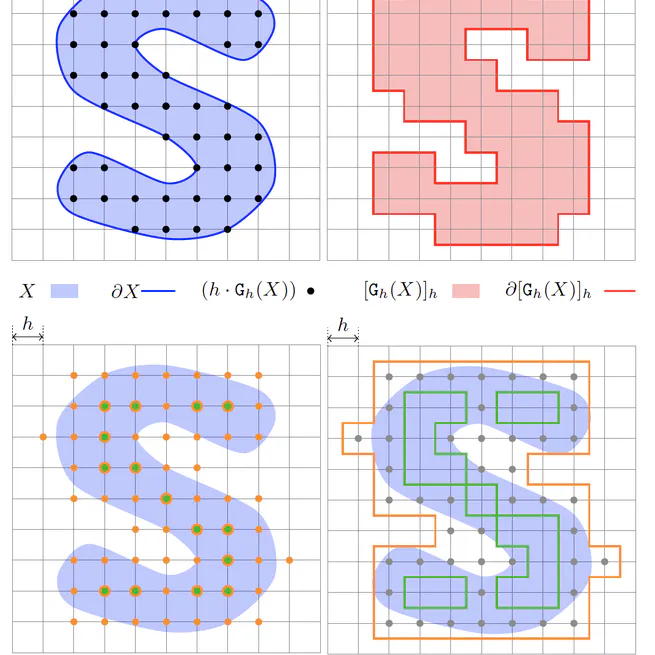
Convergent Geometric Estimators with Digital Volume and Surface Integrals
Jan 1, 2016
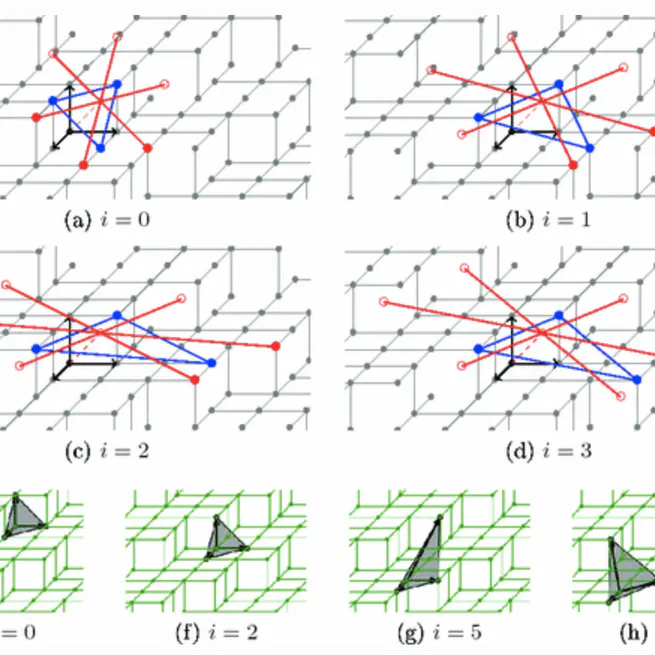
Computation of the Normal Vector to a Digital Plane by Sampling Significant Points
Jan 1, 2016
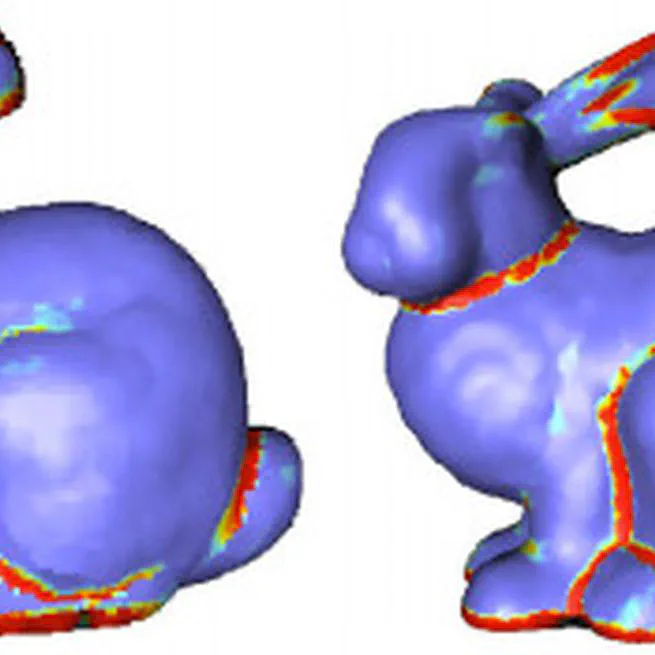
Voronoi-Based Geometry Estimator for 3D Digital Surfaces
Jan 1, 2014
Maximal Planes and Multiscale Tangential Cover of 3D Digital Objects
Jan 1, 2011
Geometric measures on arbitrary dimensional digital surfaces
Jan 1, 2003