Convergent Geometric Estimators with Digital Volume and Surface Integrals

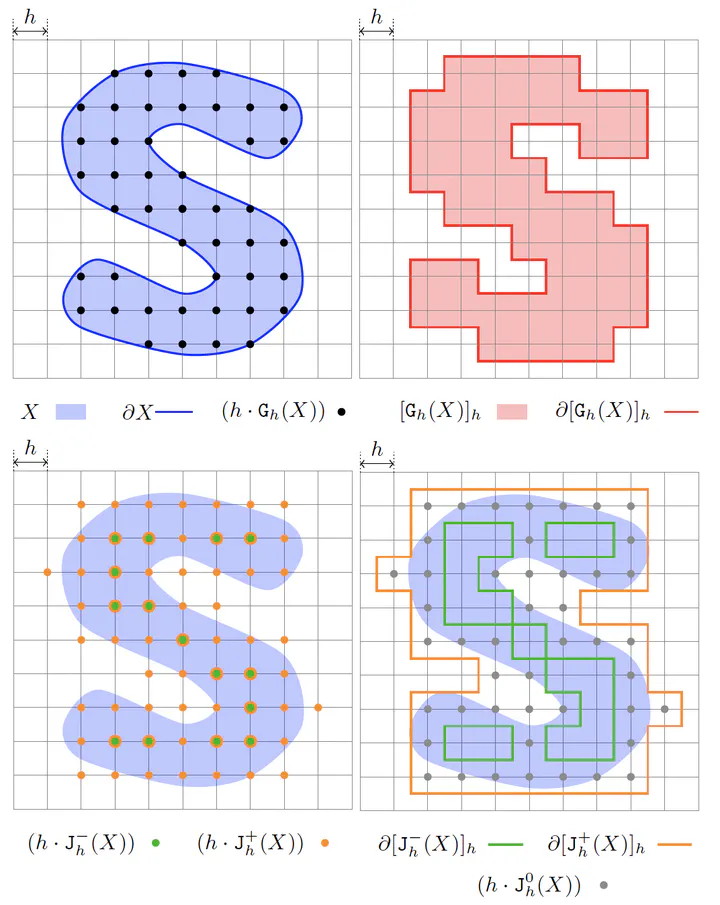
Abstract

This talk presents several methods to estimate geometric quantities on subsets of the digital space Zd. We take an interest both on global geometric quantities like volume and area, and on local geometric quantities like normal and curvatures. All presented methods have the common property to be multigrid convergent, i.e. the estimated quantities tend to their Euclidean counterpart on  ner and  ner digitizations of (smooth enough) Euclidean shapes. Furthermore, all methods rely on digital integrals, which approach either volume integrals or surface integrals along shape boundary. With such tools, we achieve multigrid convergent estimators of volume, moments and area in Zd, of normals, curvature and curvature tensor in Z2 and Z3, and of covariance measure and normals in Zd even with Hausdorff noise.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.