Experimental Comparison of Continuous and Discrete Tangent Estimators Along Digital Curves

Abstract

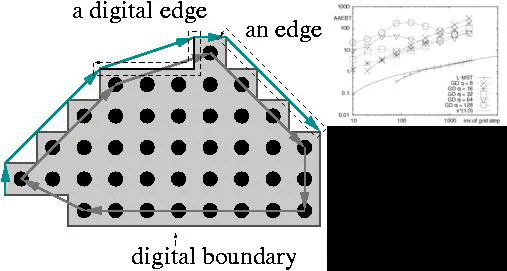
Estimating the geometry of a digital shape or contour is an important task in many image analysis applications. This paper proposes an in-depth experimental comparison between various continuous tangent estimators and a representative digital tangent estimator. The continuous estimators belong to two standard approximation methods: least square fitting and gaussian smoothing. The digital estimator is based on the extraction of maximal digital straight segments [Lachaud05a,Lachaud06d]. The comprehensive comparison takes into account objective criteria such as isotropy and multigrid convergence. Experiments underline that the proposed digital estimator addresses many of the proposed objective criteria and that it is in general as good - if not better - than continuous methods.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.