Abstract
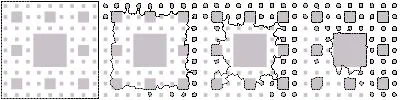
Deformable models like snakes are a classical tool for image segmentation. Highly deformable models extend them with the ability to handle dynamic topological changes, and therefore to extract arbitrary complex shapes. However, the resolution of these models largely depends on the resolution of the image. As a consequence, their time and memory complexity increases at least as fast as the size of input data. In this paper we extend an existing highly deformable model, so that it is able to locally adapt its resolution with respect to its position. With this property, a significant precision is achieved in the interesting parts of the image, while a coarse resolution is maintained elsewhere. The general idea is to replace the Euclidean metric of the image space by a deformed non-Euclidean metric, which geometrically expands areas of interest. With this approach, we obtain a new model that follows the robust framework of classical deformable models, while offering a significant independence from both the size of input data and the geometric complexity of image components.
Jacques-Olivier Lachaud
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.