Circular arc reconstruction of digital contours with chosen Hausdorff error

Abstract

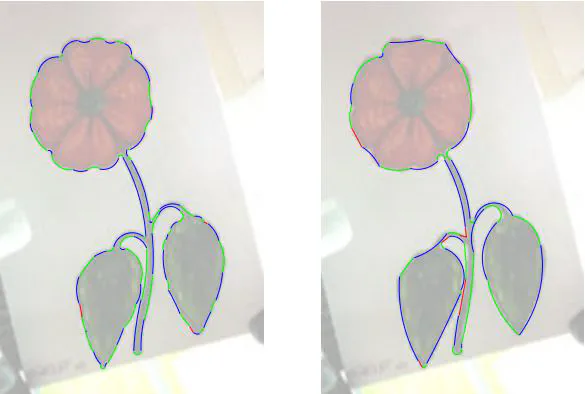
We address the problem of constructing an approximate continuous representation of a digital contour with guarantees on the Hausdorff error between the digital shape and its reconstruction. Instead of polygonalizing the contour, we propose to reconstruct the shape with circular arcs. To do so, we exploit the recent curvature estimators. From their curvature field, we introduce a new simple and efficient algorithm to approximate a digital shape with as few arcs as possible at a given scale, specified by a maximal admissible Hausdorff distance. We show the potential of our reconstruction method with numerous experiments and we also compare our results with some recent promising approaches. Last, all these algorithms are available online for comparisons on arbitrary shapes.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.