Numerical implementation of the Ambrosio-Tortorelli functional using discrete calculus and application to image restoration and inpainting

Abstract

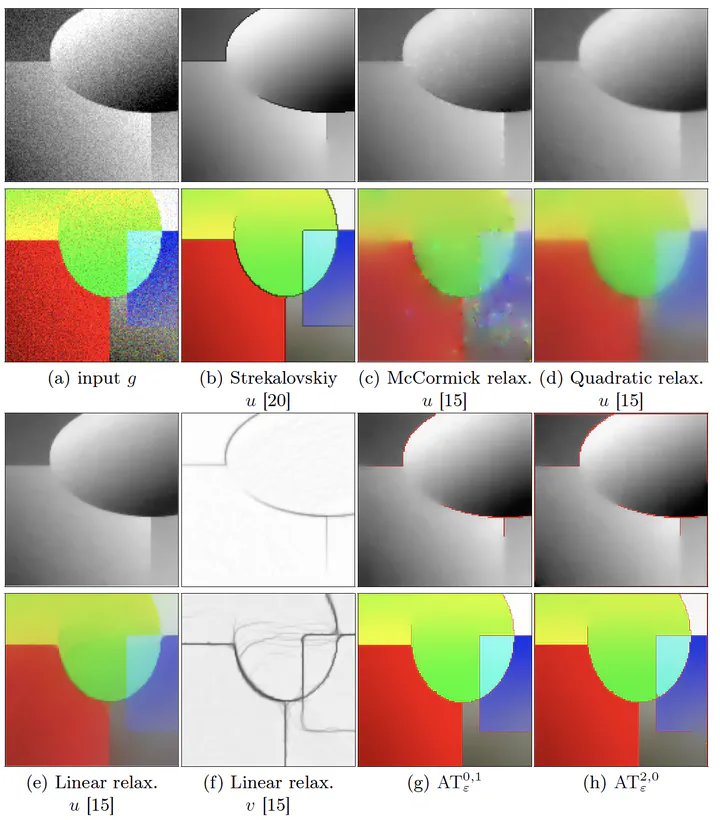
The Mumford-Shah (MS) functional is one of the most influential variational model in image segmentation, restoration, and cartooning. Difficult to solve, the Ambrosio-Tortorelli (AT) functional is of particular interest, because minimizers of AT can be shown to converge to a minimizer of MS. This paper takes an interest in a new method for numerically solving the AT model [11]. This method formulates the AT functional in a discrete calculus setting, and by this way is able to capture the set of discontinuities as a one-dimensional set. It is also shown that this model is competitive with total variation restoration methods. We present here the discrete AT models in details, and compare its merit with recent convex relaxations of AT and MS functionals. We also examine the potential of this model for inpainting, and describe its implementation in the DGtal library, an open-source project.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.