Abstract
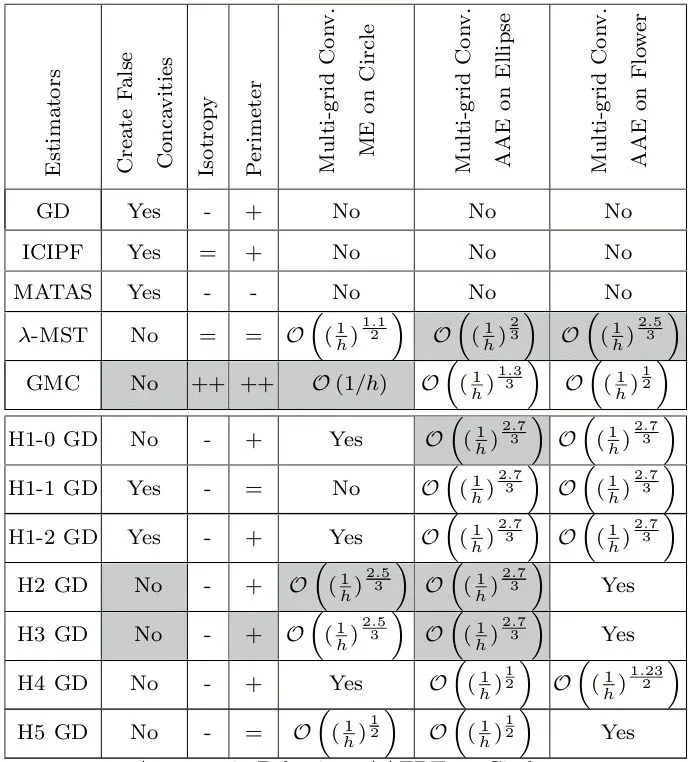
Many contour-based applications rely on the estimation of the geometry of the shape, such as pattern recognition or classification methods. This paper proposes a comprehensive evaluation on the problem of tangent estimators on digital curves. The methods taken into account use different paradigms : approximation and digital geometry. In the former paradigm, methods based on polynomial fitting, smoothing and filtering are reviewed. In the latter case of digital geometry, we consider two methods that mainly rely on digital straight line recognition [Lachaud06d] and optimization [Kerautret08a]. The comparison takes into account objective criteria such as multi-grid convergence, average error, maximum error, isotropy and length estimation. Experiments underline that adaptive methods based on digital straight line recognition often propose a good trade-off between time and precision and that if precision is to be sought, non-adaptive methods can be easily transformed into adaptive methods
Jacques-Olivier Lachaud
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.