Voronoi-Based Geometry Estimator for 3D Digital Surfaces

Abstract

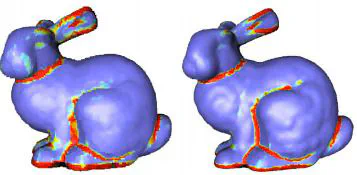
We propose a robust estimator of geometric quantities such as normals, curvature directions and sharp features for 3D digital surfaces. This estimator only depends on the digitisation gridstep and is defined using a digital version of the Voronoi Covariance Measure, which exploits the robust geometric information contained in the Voronoi cells. It has been proved in [1] that the Voronoi Covariance Measure is resilient to Hausdorff noise. Our main theorem explicits the conditions under which this estimator is multigrid convergent for digital data. Moreover, we determine what are the parameters which maximise the convergence speed of this estimator, when the normal vector is sought. Numerical experiments show that the digital VCM estimator reliably estimates normals, curvature directions and sharp features of 3D noisy digital shapes.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.