Digital Deformable Model Simulating Active Contours

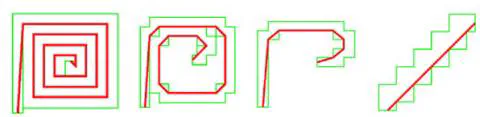
Deformable models are continuous energy-minimizing techniques that have been successfully applied to image segmentation and tracking since twenty years. This paper defines a novel purely digital deformable model (DDM), whose internal energy is based on the minimum length polygon (MLP). We prove that our combinatorial regularization term has “convex” properties: any local descent on the energy leads to a global optimum. Similarly to the continuous case where the optimum is a straight segment, our DDM stops on a digital straight segment. The DDM shares also the same behaviour as its continuous counterpart on images.

Proc. International Conference on Discrete Geometry for Computer Imagery (DGCI2009), Montréal, Québec, volume 5810 of Lecture Notes in Computer Science, pp 203-216, 2009. Springer