Convex shapes and convergence speed of discrete tangent estimators
Abstract
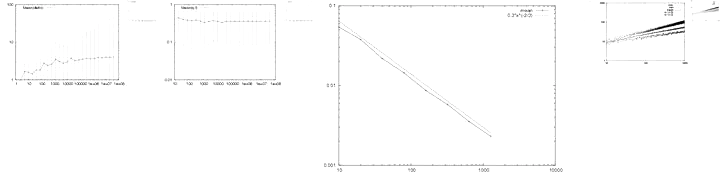
Discrete geometric estimators aim at estimating geometric characteristics of a shape with only its digitization as input data. Such an estimator is multigrid convergent when its estimates tend toward the geometric characteristics of the shape as the digitization step h tends toward 0. This paper studies the multigrid convergence of tangent estimators based on maximal digital straight segment recognition. We show that such estimators are multigrid convergent for some family of convex shapes and that their speed of convergence is on average O(h2/3). Experiments confirm this result and suggest that the bound is tight.
Type
Publication
Proc. Int. Symposium on Visual Computing (ISVC'2006), Lake Tahoe, Nevada, volume 4292 of Lecture Notes in Computer Science, pp 688-697, 2006. Springer
Digital Geometry
Discrete Geometric Estimator
Tangent Estimation
Maximal Segments
Digital Straightness
Tangential Cover
Digital Convexity
2D
Multigrid Convergence
Authors
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.