1 - Objectifs, pointeurs utiles

L'objectif de ce TP est de vous familiariser avec l'informatique graphique, d'une part avec quelques petits traitements OpenGL, d'autre part avec un peu d'algorithmique sur des modèles géométriques simples. Le langage utilisé sera le C++. On utilisera pour l'interface graphique la bibliothèque libQGLViewer. Celle-ci utilise Qt et OpenGL. L'avantage de ne pas faire de l'OpenGL directement est que libQGLViewer gère déjà pour vous la caméra, ainsi que le déplacement de la caméra. A l'issue de cette séance, vous maîtriserez:

l'affichage de triangles via OpenGL (méthode old-school OpenGL1 & 2)
un modèle géométrique simple : la soupe de triangles
le problème de l'illumination "réaliste" de triangles
un algorithme de compression out-of-core de soupes de triangles
l'écriture C++ de petites classes de calcul (points/vecteurs, indexes) avec de la surcharge d'opérateurs.

L'objectif du TP est:

de pouvoir charger en mémoire un fichier texte contenant une soupe de triangles
de pouvoir visualiser ces triangles
de fabriquer une nouvelle soupe de triangles qui approche la soupe de triangles en entrée mais qui comporte moins de triangles (compression).
d'enregistrer le résultat sous forme de fichier texte.

Les sites suivants pourront être utile pendant le TP:

[https://github.com/GillesDebunne/libQGLViewer Site libQGLViewer: exemples, doc, références]
[https://en.cppreference.com/w/ Référence C++: description détaillée des bibliothèques]
[http://www.cplusplus.com/ Site C++: tutoriels, références]
[http://www.parashift.com/c++-faq-lite/index.html C++ FAQ]

2 - Code initial, application minimale libQGLViewer

On vous donne trois fichiers main.cpp, Viewer.h, Viewer.cpp, et un fichier de configuration Qt viewer.pro. Il faut donc avoir installé libqglviewer-dev et Qt (qt5 ou qt6). A priori, tout le code peut marcher sous Windows ou MacOS. On utilise qmake pour construire un Makefile à partir du fichier viewer.pro. Le fichier a la forme ci-dessous, à adapter selon votre configuration:

# Ceci est un fichier de configuration pour une application Qt
# Il faut peut-etre legerement l adapter pour votre ordinateur.
 
# nom de votre executable
TARGET  = viewer
# config de l executable
QMAKE_CXXFLAGS = --std=c++11
CONFIG *= qt opengl release c++11
 
# config de Qt
QT *= xml opengl widgets gui
# Spécifique à Qt6
equals (QT_MAJOR_VERSION, 6) {
        QT *= gui widgets openglwidgets
        }
 
# Noms de vos fichiers entete
HEADERS = Viewer.h
# Noms de vos fichiers source (vous pouvez en mettre dautres)
SOURCES = Viewer.cpp main.cpp
 
###########################################################
# Commentez/decommentez selon votre config/systeme
# (Une config windows est possible)
###########################################################
 
# Exemple de configuration Linux de Qt et libQGLViewer Qt5
# Ubuntu 20.04
LIBS *= -L/usr/lib/x86_64-linux-gnu -lQGLViewer-qt5
 
# Exemple de configuration MacOSX avec macports
# INCLUDEPATH *= /opt/local/include
# LIBS *= -L/opt/local/lib -lQGLViewer 
 
# Exemple de configuration MacOSX/Qt5 ou Qt6 avec frameworks
# INCLUDEPATH *= /Users/me/local/src/libQGLViewer-2.9.1
# LIBS *= -F/Users/me/local/src/libQGLViewer-2.9.1/QGLViewer -framework QGLViewer
 
# Exemple de configuration Windows :
# LIBS *= -lopengl32 -lglu32
# INCLUDEPATH *= D:\Cours\Info805\TP1\libQGLViewer-2.7.1
# LIBS *= -LD:\Cours\Info805\TP1\libQGLViewer-2.7.1\QGLViewer -lQGLViewer2

Tapez donc

$ qmake
$ make

L'application viewer est construite et vous pouvez l'exécuter.

Note: Installation de Qt et QGLViewer sous Ubuntu 16.04 - 20.04. Il suffit d'installer les paquets qt5-default et libqglviewer-dev. On peut ensuite utiliser le fichier viewer.pro tel quel.; Pour Qt5, testé sous MacOS avec Qt5.15.8 et libQGLViewer-2.7.2. Pour Qt6, testé sous MacOS avec Qt6.4.2 et libQGLViewer-2.9.1.

Warning: Faite attention à ne pas avoir plusieurs versions de Qt5/Qt6, notamment sous MacOS. Les exécutables MacOS cherchent les bibliothèques dépendantes à leur exécution dans des séries de répertoire, pas forcément dans l'ordre que vous souhaitez. install_name_tool -add_rpath PATH peut être utile.

Regardez maintenant les fichiers Viewer.h et Viewer.cpp.

/// \file Viewer.h
#include <vector>
#include <QGLViewer/qglviewer.h>
 
class Viewer : public QGLViewer
{
 public:
  Viewer() : QGLViewer() {}
  
 protected :
  /// Called at each draw of the window
  virtual void draw();
  /// Called before the first draw
  virtual void init();
  /// Called when pressing help.
  virtual QString helpString() const;
};

/// \file Viewer.cpp
#include "Viewer.h"
 
using namespace std;
 
// Draws a tetrahedron with 4 colors.
void Viewer::draw()
{
  float colorBronzeDiff[4] = { 0.8, 0.6, 0.0, 1.0 };
  float colorRedDiff   [4] = { 1.0, 0.0, 0.0, 1.0 };
  float colorGreenDiff [4] = { 0.0, 1.0, 0.0, 1.0 };
  float colorBlueDiff  [4] = { 0.0, 0.0, 1.0, 1.0 };
 
  // Draws triangles given by 3 vertices.
  glBegin(GL_TRIANGLES);
  glColor4fv(colorBronzeDiff);
  glVertex3f( 0.0, 0.0, 0.0 );
  glVertex3f( 1.0, 0.0, 0.0 );
  glVertex3f( 0.0, 1.0, 0.0 );
  glColor4fv(colorRedDiff);
  glVertex3f( 1.0, 0.0, 0.0 );
  glVertex3f( 0.0, 1.0, 0.0 );
  glVertex3f( 0.0, 0.0, 1.0 );
  glColor4fv(colorGreenDiff);
  glVertex3f( 0.0, 0.0, 0.0 );
  glVertex3f( 0.0, 1.0, 0.0 );
  glVertex3f( 0.0, 0.0, 1.0 );
  glColor4fv(colorBlueDiff);
  glVertex3f( 0.0, 0.0, 0.0 );
  glVertex3f( 1.0, 0.0, 0.0 );
  glVertex3f( 0.0, 0.0, 1.0 );
  glEnd();
}
 
 
void Viewer::init()
{
  // Restore previous viewer state.
  restoreStateFromFile();
 
  // Opens help window
  help();
}
 
QString Viewer::helpString() const
{
  QString text("<h2>S i m p l e V i e w e r</h2>");
  text += "Use the mouse to move the camera around the object. ";
  text += "You can respectively revolve around, zoom and translate with the three mouse buttons. ";
  text += "Left and middle buttons pressed together rotate around the camera view direction axis<br><br>";
  text += "Pressing <b>Alt</b> and one of the function keys (<b>F1</b>..<b>F12</b>) defines a camera keyFrame. ";
  text += "Simply press the function key again to restore it. Several keyFrames define a ";
  text += "camera path. Paths are saved when you quit the application and restored at next start.<br><br>";
  text += "Press <b>F</b> to display the frame rate, <b>A</b> for the world axis, ";
  text += "<b>Alt+Return</b> for full screen mode and <b>Control+S</b> to save a snapshot. ";
  text += "See the <b>Keyboard</b> tab in this window for a complete shortcut list.<br><br>";
  text += "Double clicks automates single click actions: A left button double click aligns the closer axis with the camera (if close enough). ";
  text += "A middle button double click fits the zoom of the camera and the right button re-centers the scene.<br><br>";
  text += "A left button double click while holding right button pressed defines the camera <i>Revolve Around Point</i>. ";
  text += "See the <b>Mouse</b> tab and the documentation web pages for details.<br><br>";
  text += "Press <b>Escape</b> to exit the viewer.";
  return text;
}

La méthode Viewer::draw est appelée chaque fois que nécessaire (par exemple à chaque déplacement de la caméra). C'est elle qui envoie les ordres d'affichage à OpenGL, via les commandes glBegin, glColor, glVertex, etc. Notez que les commandes de positionnement de la caméra et de la transformation perspective sont faites par libQGLViewer (donc la classe qglviewer::QGLViewer).

Ainsi, pour afficher des triangles, vous n'aurez qu'à donner les coordonnées des 3 sommets de chacun des triangles.

3 - Soupe de triangles

On va se donner en entrée des fichiers contenant des triangles décrits sous format texte (c'est pas optimisé, mais c'est pas grave). Par ligne, on aura les 3 coordonnées des 3 sommets de chaque triangle, soit 9 nombres à virgule flottante. Les lignes commençant par '#' seront des commentaires.

# Soupe 1 ...
5.40414 0.269732 0.917559 4.68585 0.381459 0.739248 4.35375 -1.08202 1.25418
5.40414 0.269732 0.917559 4.35375 -1.08202 1.25418 5.02057 -1.34041 1.47509
4.68585 0.381459 0.739248 4.26875 0.269732 0.127895 3.9607 -1.10742 0.617722
4.68585 0.381459 0.739248 3.9607 -1.10742 0.617722 4.35375 -1.08202 1.25418
4.26875 0.269732 0.127895 4.39716 0 -0.558376 4.07166 -1.40172 -0.0614581
4.26875 0.269732 0.127895 4.07166 -1.40172 -0.0614581 3.9607 -1.10742 0.617722
4.39716 0 -0.558376 4.99586 -0.269732 -0.917559 4.62163 -1.79253 -0.385507
4.39716 0 -0.558376 4.62163 -1.79253 -0.385507 4.07166 -1.40172 -0.0614581
4.99586 -0.269732 -0.917559 5.71414 -0.381459 -0.739248 5.28845 -2.05092 -0.164601
4.99586 -0.269732 -0.917559 5.28845 -2.05092 -0.164601 4.62163 -1.79253 -0.385507
5.71414 -0.381459 -0.739248 6.13125 -0.269732 -0.127895 5.68151 -2.02552 0.471856
# etc

3.1 - Classes de base

Faites un fichier Utils.h (éventuellement aussi Utils.cpp) dans lequel vous allez mettre un peu toutes vos classes.

Commencez par créer une classe Vecteur qui contient quelques fonctions de base pour manipuler 3 flottants.

#include <iostream>
 
// Utils.h
struct Vecteur {
  float xyz[ 3 ]; // les composantes
  Vecteur( float x, float y, float z ); // constructeur
  float  operator[]( int i ) const;     // accesseur en lecture
  float& operator[]( int i );           // accesseur en ecriture
};
std::ostream& operator<<( std::ostream& out, Vecteur v );
std::istream& operator>>( std::istream& in, Vecteur& v );

// Utils.cpp
std::ostream& operator<<( std::ostream& out, Vecteur v )
{
  out << v[ 0 ] << " " << v[ 1 ] << " " << v[ 2 ];
  return out;
}
std::istream& operator>>( std::istream& in, Vecteur& v )
{
  in >> v[ 0 ] >> v[ 1 ] >> v[ 2 ];
  return in;
}

Faites ensuite une classe Triangle qui se compose de 3 vecteurs, les sommets du triangle. On peut aussi créer des opérateurs flux pour la classe triangle, sur le même principe que ci-dessus.

3.2 - Classe TriangleSoup et chargement.

Ecrivez maintenant la classe TriangleSoup qui comporte au moins les méthodes et attributs suivants:

struct TriangleSoup {
  std::vector<Triangle> triangles; // les triangles
  TriangleSoup() {}
  void read( std::istream& in );
};

Vous allez avoir besoin d'inclure les entêtes systèmes iostream, fstream, sstream. On rappelle que pour obtenir le flux en lecture sur le fichier "toto.tri", on écrit:

ifstream input( "toto.tri" ); // input est un flux en entrée.
if ( ! input.good() ) std::cerr << "ERROR" << std::endl;
...
inputFile.close(); // à la fin

Note: Pour lire une ligne à la fois dans le flux, utilisez getline( istream, string ) dans une chaîne de caractères str. Ensuite, créez un istringstream autour de str pour voir la chaîne comme un flux d'entrée, et passez ce flux à l'operateur >> de Triangle.

std::string line;
std::getline( input, line );
if ( ( line.size() > 0 ) && ( line[ 0 ] != '#' ) )  {
  std::istringstream inputLine( line );
  float x,y,z;
  inputLine  >> x >> y >> z;
   ...
}   

Il ne vous reste plus qu'à écrire la méthode read pour lire les triangles dans le flux en entrée. Transformez votre main pour qu'il récupère en premier paramètre (argv[1]) le nom du fichier contenant les triangles. Je vous donne ci-dessous des pointeurs vers des soupes de triangles.

un noeud de trèfle https:./tref.tri (50Ko)
un modèle pixelisé (gzipped) du célèbre Stanford bunny https:./bunny258.tri.gz (3.4Mo)
une surface extraite (gzipped) par Marching-cubes d'une image CT 3d https:./cthead100.tri.gz (5.4Mo)
un modèle pixelisé (gzipped) de "Octaflower" https:./octaflower-513.tri.gz (8.5Mo)
un modèle pixelisé (gzipped) de "RepublicCruiser" https:./rcruiser.tri.gz (2.5Mo)

Vous vérifiez que ça fonctionne en affichant le nombre de triangles dans votre classe TriangleSoup après chargement.

3.2 - Classe TriangleSoup et chargement.

On modifie maintenant la classe Viewer en lui rajoutant un pointeur vers un TriangleSoup, et en rajoutant au constructeur un paramètre TrangleSoupe:

class Viewer : public QGLViewer
{
 public:
  TriangleSoup* ptrSoup;
 
  Viewer( TriangleSoup* aSoup = 0 ) : QGLViewer(), ptrSoup( aSoup ) {}
...
};

Modifiez maintenant la fonction Viewer::draw pour qu'elle affiche tous les triangles de la soupe, au lieu du tétraèdre.

TriangleSoup iSoup;
ifstream input( "tref.tri" );
iSoup.read( input );
viewer.ptrSoup = &soup;
viewer.setWindowTitle("Viewer triangle soup");
...

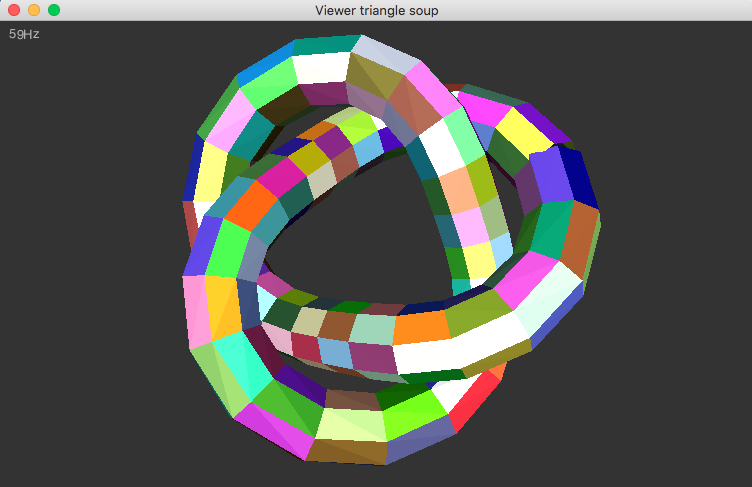
Voilà un aperçu de ce que ça donne sur "tref.tri", si vous avez choisi la couleur bronze.

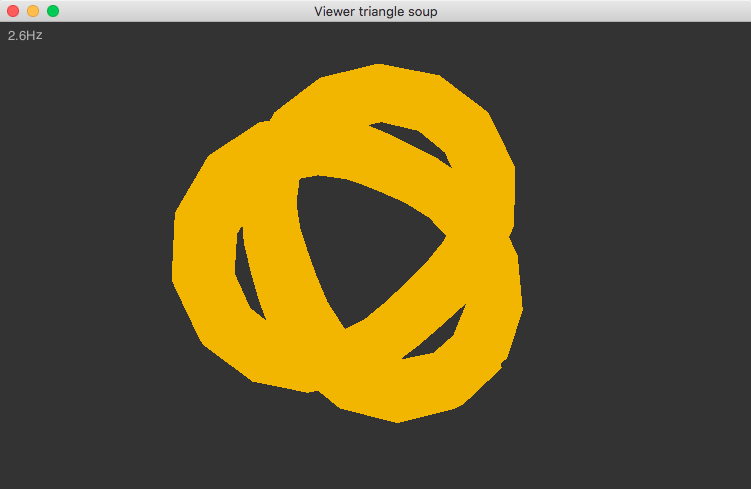
Il y a normalement plusieurs problèmes:

d'abord, on voit que les couleurs sont "pleines" sur les faces, et on n'a pas l'impression de volume;
ensuite il est possible que l'on ne voit pas tout le volume, selon le paramétrage de la caméra ou le modèle géométrique lu en entrée.

On va les résoudre dans les questions suivantes.

3.3 - Ajustement de la caméra

Il faut préciser à la caméra la taille et la position de l'objet à regarder pour qu'elle embrasse toute la scène au début. C'est en fait relativement complexe si on devait le faire sur les matrices de transformation, mais tout simple grâce à QGLViewer.

Il suffit juste de calculer la boîte englobante à l'objet (ici la soupe de triangles), et de la donner au Viewer. Pour ce faire, écrivez d'abord les deux méthodes suivantes dans Vecteur, qui vont servir à calculer les deux points extrêmes qui définissent une boîte englobante (l'un est le inf de tous les vecteurs, l'autre est le sup de tous les vecteurs):

struct Vecteur {
...
  // Retourne le vecteur dont les composantes sont les minima des
  // composantes de soi-même et de other.
  Vecteur inf( const Vecteur& other ) const;
  // Retourne le vecteur dont les composantes sont les maxima des
  // composantes de soi-même et de other.
  Vecteur sup( const Vecteur& other ) const;
...

En utilisant les 2 méthodes ci-dessus, écrivez ensuite la méthode void TriangleSoup::boundingBox( Vecteur& low, Vecteur& up) qui calcule la boîte qui englobe tous les sommets de la soupe de triangle.

Il ne reste plus qu'à appeler dans la méthode Viewer::init, la méthode boundingBox suivie de la méthode qui règle la camera.

// dans Viewer::init
  camera()->setSceneBoundingBox( ... );
// ou camera()->setSceneRadius( ... );
  camera()->showEntireScene( ... );

3.4 - Flat shading sur les faces

Pour que OpenGL puisse calculer une couleur qui dépend de l'éclairage et de la position de la caméra, il faut lui donner d'abord une information supplémentaire : le vecteur normal à la surface, donc ici, à chacun à des triangles. Pour un triangle abc donné, nous allons le calculer simplement en faisant le produit vectoriel \( \vec{ab} \times \vec{ac} \). Ecrivez donc la méthode Vecteur::cross qui calcule le produit vectoriel entre soi-même et un autre vecteur donné en paramètre.

Note: On note que si \( \vec{u} \) et \( \vec{v} \) sont deux vecteurs alors leur produit vectoriel \( \vec{w} = \vec{u} \times \vec{v} \) s'écrit en composantes:

\[ \begin{pmatrix} w_x \\ w_y \\ w_z \end{pmatrix} = \begin{pmatrix} u_y v_z - u_z v_y \\ u_z v_x - u_x v_z \\ u_x v_y - u_y v_x \end{pmatrix} \]

Note: Voir wikipedia pour le calcul et les propriétés. On utilise ici juste le fait que le vecteur \( \vec{ab} \times \vec{ac} \) est orthogonal au triangle \( abc \).

struct Vecteur { ...
  Vecteur cross( const Vecteur& v ) const;
  ...
};

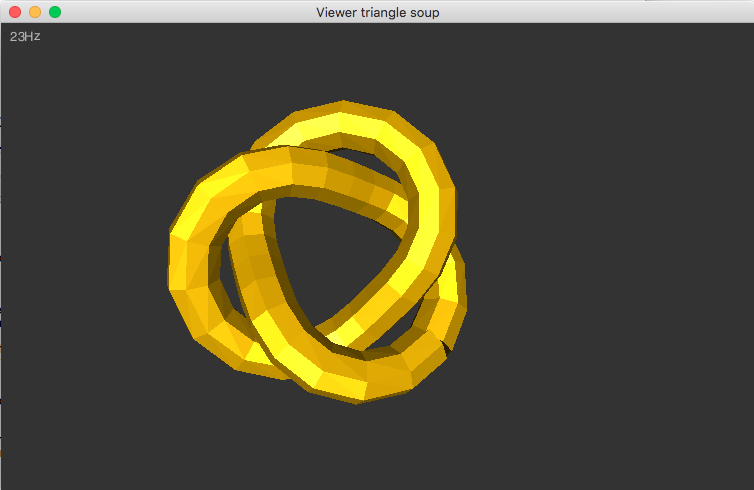
Ecrivez ensuite une méthode Vecteur Triangle::normal() const qui retourne le vecteur normal au triangle (n'oubliez pas de normaliser le vecteur pour qu'il ait une norme 1. Il suffit enfin de rajouter dans Viewer::draw les lignes suivantes:

...
  float colorBronzeDiff[4] = { 0.8, 0.6, 0.0, 1.0 };
  float colorBronzeSpec[4] = { 1.0, 1.0, 0.4, 1.0 };
  float colorNull      [4] = { 0.0, 0.0, 0.0, 1.0 };
 
  // OpenGL met en place par défaut le modèle de Phong d'illumination.
  glBegin(GL_TRIANGLES);
  // Si vous les écrivez là, ces couleurs/réglages seront partagés par tous
  // les triangles. 
  glColor4fv(colorBronzeDiff);
  glMaterialfv(GL_FRONT, GL_DIFFUSE, colorBronzeDiff);
  glMaterialfv(GL_FRONT, GL_SPECULAR, colorBronzeSpec);
  glMaterialf(GL_FRONT, GL_SHININESS, 20.0f );
  ...
    // Pour chaque triangle, avant les glVertex de chaque triangle:
    const Triangle& T = ptrSoup->triangles[ i ];
    Vecteur n = T.normal();
    glNormal3f( n[ 0 ], n[ 1 ], n[ 2 ] );
    glVertex
  ...

Vous devriez maintenant avoir votre visualisateur de soupes de triangles qui ressemble à ceci :

3.5 - Couleur ambiente / diffuse / spéculaire

En fait, tel qu'écrit plus haut, vous avez donné une couleur ambiente "bronze" (donc c'est le minimum de couleur, même dans le noir), à laquelle vous ajoutez encore une couleur diffuse "bronze" (dépend de la lumière), et enfin une couleur spéculaire jaune, mais très brillant (donc assez métallique). Si vous voulez un effet très métallique, mettez la couleur ambiente à (0,0,0). Vous devriez obtenir:

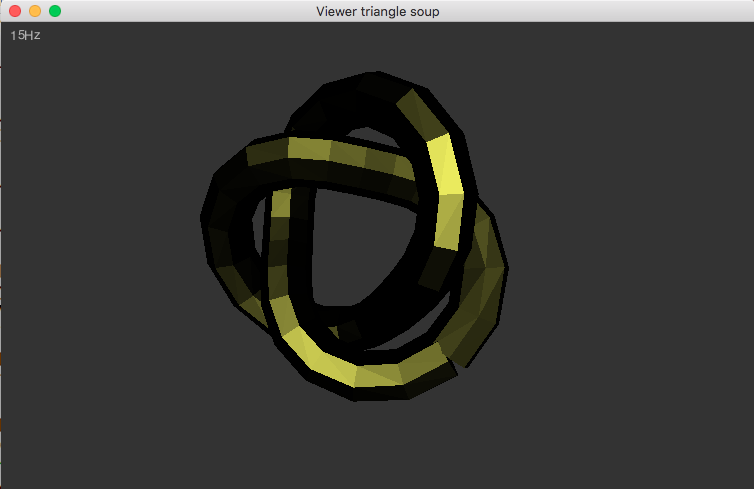
Vous pouvez jouer un peu avec les paramètres pour voir les différents effets possibles.

Si vous voulez changer les matériaux de chacun des triangles, il faut le dire à OpenGL après glBegin(GL_TRIANGLES) avec:

glBegin(GL_TRIANGLES);
glEnable(GL_COLOR_MATERIAL); // le materiau peut changer à chaque triangle.
... 
// changer les couleurs à chaque triangle.
...
glDisable(GL_COLOR_MATERIAL);
glEnd();

On peut par exemple obtenir un effet "Elmer" en utilisant la partie décimale des coordonnées d'un sommet comme couleur ambiente.

4 - Compression par découpage sur une grille régulière

Nous allons maintenant implémenter un algorithme de compression de soupes de triangles, qui est d'une part entièrement parallélisable, et d'autre part peut même fonctionner sous forme de flux d'entrée-sortie. Chaque triangle sera en effet traité indépendamment des autres.

4.1 - Principe de l'algorithme

On va découper l'espace (enfin, la boîte englobante de l'objet) de façon régulière en une grille. Un paramètre de l'algorithme de compression est le nombre de découpage selon chaque dimension, soit 3 entiers nbx, nby, nbz. Si vous choisissez (10,10,10) la boîte englobante sera découpée en \( 10 \times 10 \times 10 \) cellules, soit 1000 cellules.
Chacune de ces cellules sera en fait numérotée naturellement par un triplet d'entier, de (0,0,0) à (9,9,9). Ce triplet sera appelé Index de la cellule.
Ensuite, on cherchera dans quelle cellule tombe chaque sommet. Un triangle ayant 3 sommets, chacun des 3 sommets d'un triangle aura donc un Index.
Si les 3 sommets d'un triangle n'ont pas tous un Index différent, alors on jette le triangle ! Il ne sera pas dans la soupe de triangle en sortie.
1. Si les 3 sommets d'un triangle ont chacun un Index différent, on va construire un triangle de sortie. La difficulté est qu'il faut replacer les sommets si on ne veut pas avoir des trous partout dans la triangulation de sortie. Dans un premier temps, vous placerez les sommets au centre de la cellule. Dans un deuxième temps, vous placerez les sommets au barycentre de tous les sommets qui tombent dans la cellule.
2. Si 2 sommets ou 3 sommets ont le même Index, on jette le triangle.
L'ensemble des triangles de sortie forme une soupe de triangles, que l'on pourra sauvegarder dans un fichier. Cette soupe de triangles a au pire le même nombre de triangles que la soupe en entrée, et en général beaucoup moins. Dans certains cas, elle peut même lisser le résultat.

4.2 - Zipper et index d'une cellule

On va créer une classe TriangleSoupZipper pour réaliser la compression. On va se servir aussi d'une classe Index pour stocker les 3 entiers qui numérotent chaque cellule. Une partie de cette classe vous est donnée ci-dessous:

/// Définit un index sur 3 entiers. Toutes les opérations usuelles
/// sont surchargées (accès, comparaisons, égalité).
struct Index {
  int idx[ 3 ];
  Index() {}
  Index( int i0, int i1, int i2 )
  {
    idx[ 0 ] = i0;
    idx[ 1 ] = i1;
    idx[ 2 ] = i2;
  }
  Index( int indices[] )
  {
    idx[ 0 ] = indices[ 0 ];
    idx[ 1 ] = indices[ 1 ];
    idx[ 2 ] = indices[ 2 ];
  }
  int  operator[]( int i ) const { return idx[ i ]; }
  int& operator[]( int i )       { return idx[ i ]; }
  bool operator<( const Index& other ) const
  {
    return ( idx[ 0 ] < other.idx[ 0 ] )
      || ( ( idx[ 0 ] == other.idx[ 0 ] )
           && ( ( idx[ 1 ] < other.idx[ 1 ] )
                || ( ( idx[ 1 ] == other.idx[ 1 ] )
                     && ( idx[ 2 ] < other.idx[ 2 ] ) ) ) );
  }
};

Rajoutez l'opérateur d'égalité == dans la classe. Vous écrirez ensuite la classe TriangleSoupZipper avec le constructeur suivant:

struct TriangleSoupZipper { ...
  // Construit le zipper avec une soupe de triangle en entrée \a
  // anInput, une soupe de triangle en sortie \a anOutput, et un index \a size
  // qui est le nombre de cellules de la boîte découpée selon les 3 directions.
  TriangleSoupZipper( const TriangleSoup& anInput,
                      TriangleSoup& anOuput, 
                      Index size );
  ...
};

N'oubliez pas de créer les données membres nécessaires. Vous précalculerez dans le constructeur, la boîte englobante de la soupe de triangles en entrée, les tailles réelles de chaque cellule (i.e. il faut diviser la taille de la boîte par le nombre de cellules le long de chaque dimension).

Vous aurez ensuite besoin de créer une méthode index qui calcule l'Index d'un point dans l'espace, et son inverse la fonction centroid qui calcule le centroïde de la cellule d'Index donné.

/// @return l'index de la cellule dans laquelle tombe \a p.
Index index( const Vecteur& p ) const;
/// @return le centroïde de la cellule d'index \a idx (son "centre").
Vecteur centroid( const Index& idx ) const;

Note: Par exemple, si la boîte englobante est (-5,-5,-5) - (5,5,5) et qu'on a divisé en 10 x 10 x 10 cellules, alors l'index du point (1.2, 3.4, -1.7) est (6,8,3). Le centroïde de la cellule (6,8,3) est (1.5, 3.5, -1.5).

4.3 - Compression sans replacement des sommets des triangles

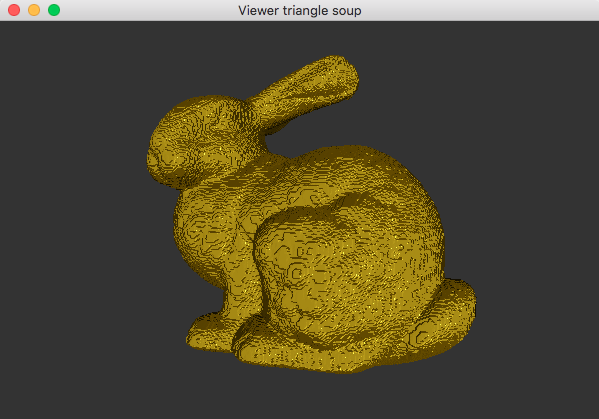
Il ne reste plus qu'à écrire une méthode zip() qui compresse tous les triangles de la soupe en entrée et sort les triangles dont les sommets ont des index différents. La position des sommets en sortie est juste centroid( idx ) si idx est l'index du sommet. Vous obtiendrez un résultat du type:


bunny258.tri (464588 triangles)	pour une décomposition 50x50x50 (19637 triangles)

4.4 - Compression avec replacement des sommets des triangles

Malheureusement le résultat n'est souvent pas très joli. Cela vient du mauvais positionnement des sommets des triangles de sortie. Une meilleure idée est de moyenner tous les sommets qui tombent dans la même cellule, puis en sortie d'associer cette position moyenne aux sommets. On va donc calculer (pendant la fonction zip()) le barycentre des sommets de chaque cellule. Ensuite, on réaffectera les positions des sommets des triangles de sortie.

Il faut donc calculer les barycentres de toutes les cellules qui touchent les triangles. On pourrait faire un grand tableau. C'est un peu lourd. On va plutôt utiliser un tableau associatif, i.e. un std::map en C++, qui va associer à un Index une structure CellData qui va stocker un accumulateur de "Point" et un nombre. Elle aura la forme suivante:

// Structure pour calculer le barycentre d'un ensemble de points.
struct CellData {
  Vecteur acc;
  int nb;
  // Crée un accumulateur vide.
  CellData(): acc(), nb(0) {}
  // Ajoute le point v à l'accumulateur.
  void add( const Vecteur& v );
  // Retourne le barycentre de tous les points ajoutés.
  Vecteur barycenter() const;
};

Ecrivez cette structure. Ensuite, ajoutez dans TriangleSoupZipper une donnée membre `index2data:

struct TriangleSoupZipper {
...
  // Stocke pour chaque cellule son barycentre.
  std::map<Index, CellData> index2data;
...
};

Mettez à jour zip() pour que chaque sommet soit ajouté au barycentre de sa cellule (mise à jour de index2data). Ecrivez enfin la méthode smartZip() qui :

Met à zéro index2data avec sa méthode clear().
Appelle zip()
Reparcourt les triangles de sortie pour replacer les sommets au barycentre de leur cellule (plutôt que leur centroïde).

Pour chaque sommet s d'un triangle de sortie, sa nouvelle position est index2data[ index( s ) ].barycenter()

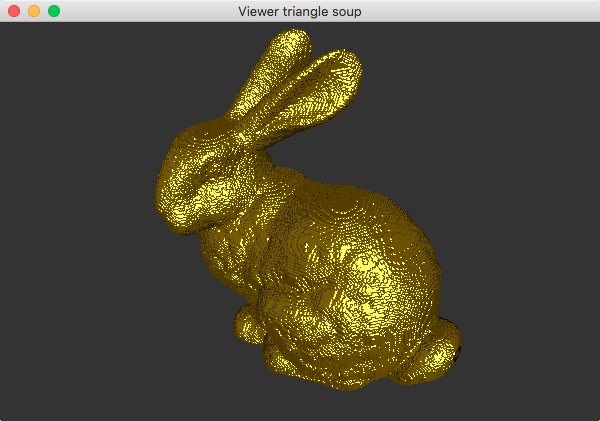
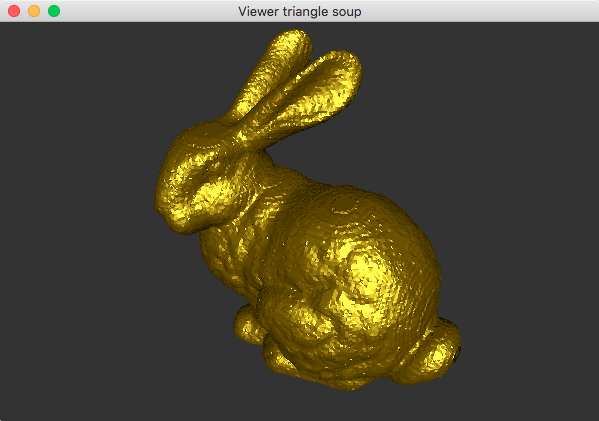
Vous devriez maintenant obtenir les résultats suivants, beaucoup plus satisfaisants:


Input : bunny258.tri (464588 triangles)	Output : pour une décomposition 20x20x20 (3184 triangles)

Output : pour une décomposition 50x50x50 (19637 triangles)	Output : pour une décomposition 100x100x100 (74060 triangles)

5 - Conclusion et remise du TP

Il ne vous reste plus qu'à faire 2 exécutables (qui peuvent être dans deux répertoires différents avec deux fichiers .pro différents):

Un visualiseur graphique viewer de soupe de triangles (1 argument: le nom du fichier contenant la soupe de triangles). Ce programme affichera le nombre de triangles en entrée.
Un programme non graphique qui prend 5 arguments, le nom du fichier contenant la soupe de triangles en entrée, le nom du fichier contenant la soupe de triangles en sortie, et les 3 entiers décrivant la subdivision. Ce programme affichera le nombre de triangles en entrée, en sortie, et le taux de compression (nb_triangles_output / nb_triangles_input * 100).

Et un README à la racine qui précise quelles sont les questions traitées complètement, partiellement, ou non-traitées.

Tout cela sera à remettre via TPLab en binôme avant dimanche 4 février minuit.

Table of Contents

1 - Objectifs, pointeurs utiles

2 - Code initial, application minimale libQGLViewer

3 - Soupe de triangles

3.1 - Classes de base

3.2 - Classe TriangleSoup et chargement.

3.2 - Classe TriangleSoup et chargement.

3.3 - Ajustement de la caméra

3.4 - Flat shading sur les faces

3.5 - Couleur ambiente / diffuse / spéculaire

4 - Compression par découpage sur une grille régulière

4.1 - Principe de l'algorithme

4.2 - Zipper et index d'une cellule

4.3 - Compression sans replacement des sommets des triangles

4.4 - Compression avec replacement des sommets des triangles

5 - Conclusion et remise du TP