1 - Objectifs

L'objectif de ce TP est de vous faire mettre en oeuvre des algorithmes efficaces pour détecter les collisions entre objets dans le plan, au travers d'une application de simulation de déplacement de particules.

Un premier moteur temps-réel de visualisation, basé sur la bibliothèque GTK (http://www.gtk.org), vous est fourni. Vous vous en êtes déjà servi en cours de C, INFO505 (http://www.lama.univ-savoie.fr/~lachaud/Cours/INFO504/Tests/doc/html/tp3.html) pour le TP Tetris graphique. Vous reconnaîtrez l'utilisation des timers et des zones de dessins pour une application animée en temps-réel.

Pas mal de choses vous sont déjà fournis, histoire de se concentrer un peu plus sur les requêtes de proximité. On vous donne les fichiers suivants:

main.c : contient l'IHM, la partie temps-réel, le calcul de la dynamique des objets, l'affichage.
points.h, points.c : la structure de point "simple", avec quelques opérations point/vecteur.
particules.h, particules.c : la structure de particules qui mémorise la position, le vecteur vitesse, les forces, la masse. On dispose aussi d'une structure de tableau dynamique de ces particules.
forces.h, forces.c : contient la structure pour représenter des forces, ici la simple gravité.

Prenez d'abord le temps de bien comprendre le code écrit. Un Makefile vous est aussi fourni.

Il s'exécute ainsi:

prompt$ make
prompt$ ./main

L'exécution du programme donne quelque chose comme ceci:

Programme initial. Des particules sont générés avec un vecteur initial et sont soumis à la gravité.

Les points suivants sont à mémoriser pour réaliser le tp:

Toute la logique du programme est gérée par la fonction tic, qui est appelée toutes les DT secondes (20 ms). Celle-ci s'occupe de générer de nouvelles particules, calculer les forces sur les particules, les déplacer, et demander le réaffichage de la zone de dessin.
Le contexte mémorise comme d'habitude tous les éléments importants de l'application.
Les particules ont leurs coordonnées réelles dans une fenêtre [-1:1]x[-1:1]. Il faut donc transformer leurs coordonnées avant affichage en coordonnées pixel, ici [0:499]x[0:499], car la zone de dessin fait 500x500. Grâce à cela, si vous voulez augmenter ou diminuer la taille de la zone de dessin, vous pouvez le faire très simplement en modifiant le contexte.

Note
Les fonctions ci-dessous, déjà écrites, vous permettent de faire le changement de repère, coordonnées réelles <-> coordonnées pixel.

Point point2DrawingAreaPoint( Contexte* pCtxt, Point p ); //< point réel -> pixel

double length2DrawingAreaLength( Contexte* pCtxt, double l ); //< longueur réelle -> longueur en pixels

Point drawingAreaPoint2Point( Contexte* pCtxt, Point p ); //< pixel -> point réel

length2DrawingAreaLength
double length2DrawingAreaLength(Contexte *pCtxt, double l)
Definition main.c:200

point2DrawingAreaPoint
Point point2DrawingAreaPoint(Contexte *pCtxt, Point p)
Definition main.c:192

drawingAreaPoint2Point
Point drawingAreaPoint2Point(Contexte *pCtxt, Point p)
Definition main.c:205

SContexte
Definition union-find.c:13

SPoint
Definition points.h:4

2 - Génération de particules plus funky

Pour rendre le reste du TP moins déterministe et plus joli visuellement, on introduit de l'aléatoire dans la génération des particules. Créez donc une fonction fontaineVariable par exemple avec le prototype ci-dessous:

void fontaineVariable( Contexte* pCtxt, 
                       double p, double var,  
                       double x, double y, double vx, double vy, double m );

Par rapport à fontaine, le paramètre var donne la variabilité sur la vitesse initiale et sur la masse. Par exemple si var vaut 0.1 alors la composante x de la vitesse à une valeur aléatoire entre (1-0.1)*vx et (1+0.1)*vx, pareil pour la composante y. Utiliser dans le générateur aléatoire rand pour créer des particules avec la variabilité var.

Par exemple, si vous placez dans tic les lignes ci-dessous pour générer les particules:

fontaineVariable( pCtxt, 0.2, 0.1, -0.5, 0.5, 0.3, 0.3, 1.0 );
fontaineVariable( pCtxt, 0.25, 0.2, -0.5, 0.5, 0.3, 0.3, 0.5 );
fontaineVariable( pCtxt, 0.6, 0.18, -0.5, 0.5, 0.3, 0.3, 2.5 );

Cela donne à peu près le résultat suivant:

Les particules sont maintenant générées avec un vecteur initial légèrement aléatoire et sont soumis à la gravité.

Note: L'expression rand() / (double) RAND_MAX vous retourne un nombre aléatoire entre 0 et 1. Faites donc une fonction rand01() qui vous retourne un nombre entre 0 et 1 ainsi:

double rand01() { return (double) rand() / (double) RAND_MAX; }

3 - Ajout d'obstacles

On va laisser l'utilisateur rajouter des obstacles (des boules) infranchissables pour nos particules, qui vont rebondir contre. Ces obstacles seront placés dans un premier temps dans un simple tableau de taille variable (comme les particules). Pour détecter si une particule rencontre un obstacle, on parcourera tous les obstacles et on vérifiera s'il y a eu collision. Dans la section suivante, on verra comment utiliser les arbres k-D pour limiter le nombre de tests de collision.

3.1 - Création d'une structure obstacle

On va créer des obstacles simples pour les particules. Ce seront des disques de rayon donné. Créez deux fichiers obstacles.h et obstacles.c pour stocker les structures de données associées aux obstacles. Un Obstacle sera donc

typedef enum { DISQUE } ObstacleType;
 
typedef struct SObstacle {
  ObstacleType type; //< Le type de l'obstacle. Ici on aura juste des DISQUEs.
  double x[ DIM ];   //< Les coordonnées du centre de l'obstacle.
  double r;          //< Le rayon de l'obstacle
  double att;        //< le facteur d'atténuation de l'obstacle (0.0 amortisseur parfait, 1.0 rebondisseur parfait, 3.0 "bumper" comme dans un flipper.)
  double cr, cg, cb; //< couleurs rgb de l'obstacle.
} Obstacle;

Sinon, vous créerez une structure TabObstacle complétement similaire à TabParticules, afin de stocker une liste d'obstacles. (Ab)usez du copier-coller pour faire les fonctions suivantes:

void TabObstacles_init( TabObstacles* tab );                  //< initialise le tableau dyn. d'obstacles
void TabObstacles_ajoute( TabObstacles* tab, Obstacle p );    //< ajoute l'obstacle p
void TabObstacles_set( TabObstacles* tab, int i, Obstacle p );//< met à jour le i-ème obstacle à p
Obstacle TabObstacles_get( TabObstacles* tab, int i );        //< retourne le i-ème obstacle
int TabObstacles_nb( TabObstacles* tab );                     //< retourne le nombre d'obstacles
Obstacle* TabObstacles_ref( TabObstacles* tab, int i );       //< retourne l'adresse du i-ème obstacle
void TabObstacles_termine( TabObstacles* tab );               //< libère les obstacles et termine le tableau
void TabObstacles_agrandir( TabObstacles* tab );              //< double la taille du tableau dynamique

N'oubliez pas de rajouter la compilation de obstacles.c dans le Makefile, ainsi que l'édition des liens de obstacles.o.

3.2 - Clic sur la zone de dessin

Pour ajouter des obstacles pour les particules, on va simplement demander à l'utilisateur de faire un clic gauche dans la zone de dessin. Pour capter un clic souris dans la zone de dessin il faut rajouter les lignes suivantes dans creerIHM :

g_signal_connect( G_OBJECT( pCtxt->drawing_area ), "button_press_event",
                  G_CALLBACK( mouse_clic_reaction ), pCtxt );
gtk_widget_set_events ( pCtxt->drawing_area, GDK_EXPOSURE_MASK
                        | GDK_LEAVE_NOTIFY_MASK
                        | GDK_BUTTON_PRESS_MASK
                        | GDK_POINTER_MOTION_MASK
                        | GDK_POINTER_MOTION_HINT_MASK);

La réaction appelée est la fonction mouse_clic_reaction, qui aura la forme suivante:

gboolean mouse_clic_reaction( GtkWidget *widget, GdkEventButton *event, gpointer data )
{
  Contexte* pCtxt = (Contexte*) data;
  int button = event->button; // 1 is left button
  if ( button != 1 ) return TRUE;
  int x = event->x;
  int y = event->y;
  ... // A compléter
  return TRUE;
}

Il vous reste donc à:

rajouter au contexte un champ TabObstacles TabO, et l'initialiser dans le main.
compléter mouse_clic_reaction pour qu'il ajoute dans TabO un nouvel Obstacle aux coordonnées cliquées. Attention il faut utiliser la fonction drawingAreaPoint2Point pour convertir les coordonnées pixel en coordonnées réelles. On choisira dans un premier temps un rayon réel r de 0.05, et une atténuation att de 0.6.
rajouter quelques lignes dans la fonction on_draw pour afficher tous les obstacles du contexte. N'oubliez pas d'utiliser la fonction de conversion de longueur réelle vers longueur pixel.

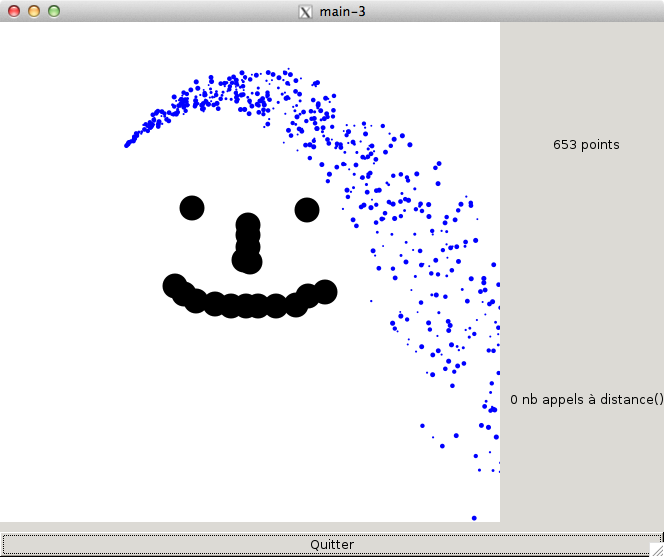
Les obstacles mis par l'utilisateur sont visibles.

3.3 - Les obstacles bloquent les particules.

Vous allez maintenant modifier la fonction deplaceParticule pour qu'elle bloque la particule si elle rencontre un obstacle. Pour faire simple dans un premier temps, vous parcourez tout le tableau d'obstacles. Dès que la distance entre les nouvelles coordonnées de la particule et un obstacle est plus petite que le rayon de l'obstacle (ici 0.05), cela veut dire que la particule est dans l'obstacle. Dans ce cas-là, vous vous contenterez de mettre à zéro la vitesse de la particule. Si la particule ne collisionne avec aucun obstacle, alors vous mettez à jour sa position comme dans la fonction deplaceParticule initiale.

Note: Vous avez déjà une fonction distance ou une fonction Point_distance dans points.c pour calculer les distances

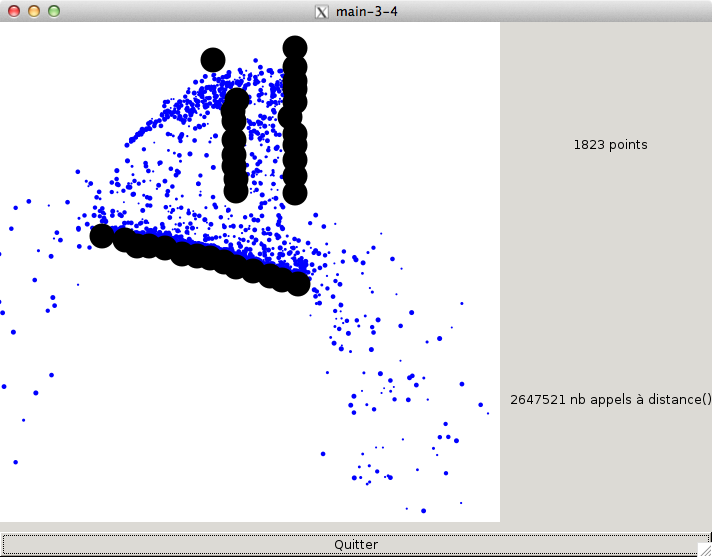
Voilà à quoi ressemble l'application maintenant:

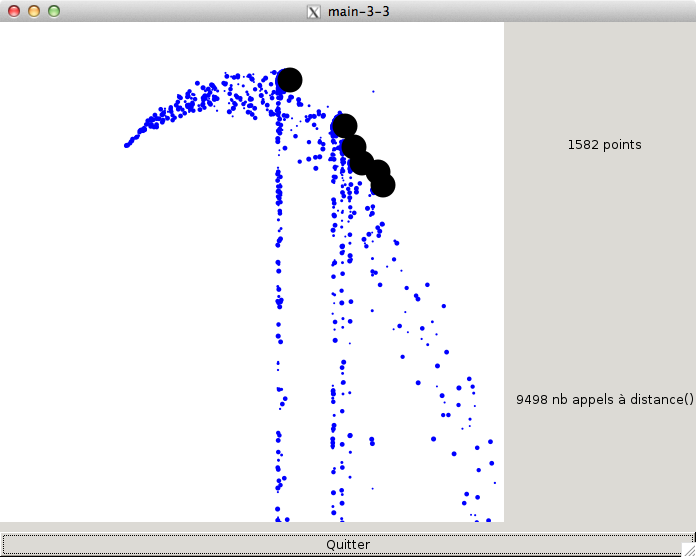
Les obstacles mis par l'utilisateur bloquent les particules.

Vous voyez maintenant le nombre de tests "distance" réalisés par seconde par l'application. Ce nombre est directement proportionnel au nombre d'obstacles et au nombre de particules.

3.4 - Les particules rebondissent sur les obstacles.

Pour que l'application soit plus réaliste, on va simuler un comportement physique des particules. En général, on rebondit sur un obstacle, comme les boules au billard rebondissent sur les côtés. Tout le calcul du rebond vous est donné dans la fonction suivante. Le principe est de simuler un rebond parfait, puis d'atténuer la force du rebond.

// Cette fonction n'est appelé que si la particule p déplacée (p.x +
// DT*p.v) est à l'intérieur du disque B_r(center).  Elle retourne
// alors le rebond de la particule calculé pour cet obstacle circulaire
// (nouveau x, nouveau v) en fonction de l'atténuation choisie.  En
// sortie, la particule est en dehors de l'obstacle.
Particule calculRebond( Particule p, Point center, double r, double att )
{
  Point xd, v;
  // Calcule la nouvelle position xd (sans collision) et le vecteur vitesse.
  xd.x[ 0 ] = p.x[ 0 ] + DT * p.v[ 0 ]; 
  xd.x[ 1 ] = p.x[ 1 ] + DT * p.v[ 1 ];
  v.x[ 0 ] = p.v[ 0 ];
  v.x[ 1 ] = p.v[ 1 ];
  Point u = Point_normalize( Point_sub( xd, center ) );
  double l = Point_norm( Point_sub( xd, center ) );
  Point xm = Point_add( center, Point_mul( r + att*( r - l), u ) );
  double proj_v = Point_dot( v, u );
  // réalise le rebond si la particule est bien en train de rentrer dans l'obstacle. 
  if ( proj_v < 0.0 ) 
    v = Point_sub( v, Point_mul( 2.0 * proj_v, u ) );
  Particule p_out = p;
  p_out.x[ 0 ] = xm.x[ 0 ];
  p_out.x[ 1 ] = xm.x[ 1 ];
  p_out.v[ 0 ] = att*v.x[ 0 ];
  p_out.v[ 1 ] = att*v.x[ 1 ];
  return p_out;
}

Il vous reste donc à modifier deplaceParticule pour qu'il utilise calculRebond en cas de rencontre avec un obstacle. Pour simplifier, on supposera que la particule rebondit sur le premier obstacle rencontré (les autres sont ignorés).

Note: Dans une simulation plus réaliste, on calcule toutes les collisions, puis on fait la moyenne des résultats de toutes les collisions. Cela donne un comportement un peu plus stable.

Les particules rebondissent sur les obstacles placés par l'utilisateur.

Note: Vous pouvez déjà vous amuser en changeant l'atténuation pour voir l'effet sur le rebond des particules.

4 - Une structure pour accélerer les tests de collision

On voit que notre simulateur doit faire un nombre considérable de tests de collision, dès lors qu'on met un certain nombre d'obstacles. Ce serait encore plus vrai si on gérait les collisions entre particules. Comme nos obstacles sont statiques (ne se déplacent pas), on va les structurer dans un arbre k-D. Du coup on n'aura pas besoin de tester pour chaque particule ses collisions possibles avec tous les obstacles.

Les arbres k-D sont des arbres binaires avec juste un fonctionnement un peu particulier. On vous donne donc les fichiers arbre.h et arbre.c, qui vous fournissent la structure Arbre et des fonctions pour créer, modifier ou se déplacer dans les arbres.

Les arbres k-D sont décrits dans la Leçon 5 d'INFO607. Les arbres k-D qui sont des arbres binaires. Chaque point situé à un noeud de l'arbre coupe l'espace en deux régions selon un plan qui dépend de la profondeur dans l'arbre. Ainsi les noeuds de profondeur 0 coupe l'espace selon leur première coordonnée \( x \), les noeuds de profondeur 1 coupe l'espace selon leur deuxième coordonnée \( y \), les noeuds de profondeur 2 coupe l'espace selon leur troisième coordonnée \( z \) en 3D, etc, en recommançant à la première coordonnée après avoir coupé selon la dernière.

Il est facile d'équilibrer les arbres k-D. Il suffit en effet à chaque fois de choisir comme point de découpe le point situé à la médiane des points restants selon la direction de découpe. Une illustration est donnée ci-dessous.

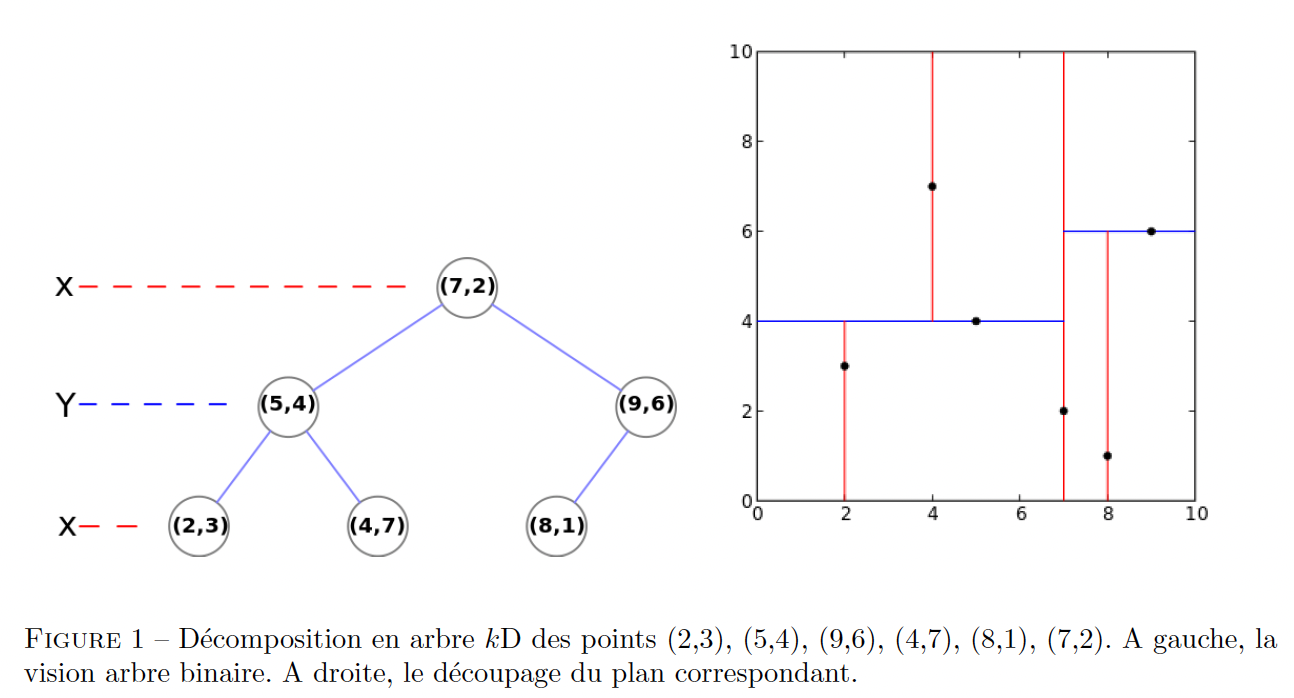
Illustration de la structure d'un k-d-tree.

4.1 - Création de l'arbre k-D des obstacles

On va donc enrichir le module arbre.h / arbre.c . Vous définirez le type Donnee comme étant un Obstacle. Il s'agira ensuite d'écrire la fonction suivante, en utilisant bien sûr les fonctions données ArbreVide, Creer0, Creer2 :

// Si T est un Obstacle* pointant vers la première case d'un tableau
// d'Obstacle, i < j désignent les indices de début et de fin dans le
// tableau T, a est l'axe (0 ou 1) utilisé pour découper le plan.
// Alors cette fonction crée et retourne l'arbre binaire (arbre k-D)
// stockant tous les obstacles spécifiés.
Arbre* KDT_Creer( Donnee* T, int i, int j, int a );

Cette fonction suit le pseudo-code de la fonction de création d'arbre k-D vue en cours:

Algorithme de création d'un arbre k-D.

Pour les fonctions MedianeSelonAxe et Partition, je vous conseille de les remplacer par une fonction de tri selon l'axe a, qui sera plus facile à écrire, quoique moins optimal. Pour le tri, vous pouvez faire un tri "maison" (genre bulle) ou utiliser qsort de stdlib.h (en utilisant une variable globale indiquant la dimension où vous triez).

Vous rajouterez alors le code suivant dans votre main:

On rajoute un champ Arbre * kdtree dans le contexte (au début initialisé à ArbreVide).
Chaque fois qu'on rajoute un Obstacle, on va recréer tout l'arbre (ce n'est pas optimal, mais en fait on ne le fait qu'à chaque clic). Donc on appelle d'abord Detruire sur l'arbre du contexte, avant d'en recréer un nouveau avec KDT_Creer qui contient un obstacle de plus.
Dans la fonction d'affichage, on appelle la fonction suivante viewerKDTree, ce qui vous permettra de déboguer votre fonction de création d'arbre.

// Affiche le K-d-tree de manière récursive, en mettant à jour la boîte
// englobante (bg, hd) correspondant à chaque noeud de l'arbre.
void viewerKDTree( Contexte* pCtxt, cairo_t* cr, 
                   Noeud* N, Point bg, Point hd, int a )
{
  if ( N != ArbreVide() )
    {
      int b = (a+1) % DIM;
      Obstacle* q = Valeur( N );
      Point p,p1,p2; 
      p1.x[ a ] = q->x[ a ];
      p1.x[ b ] = bg.x[ b ];
      p2.x[ a ] = q->x[ a ];
      p2.x[ b ] = hd.x[ b ];
      cairo_set_source_rgb( cr, 0.0, 1.0, 1.0 );
      Point draw_p1 = point2DrawingAreaPoint( pCtxt, p1 );
      Point draw_p2 = point2DrawingAreaPoint( pCtxt, p2 );
      cairo_move_to( cr, draw_p1.x[ 0 ], draw_p1.x[ 1 ] );
      cairo_line_to( cr, draw_p2.x[ 0 ], draw_p2.x[ 1 ]);
      cairo_stroke( cr );
      cairo_set_source_rgb( cr, 1.0, 0.0, 0.0 );
      p.x[ 0 ] = q->x[ 0 ]; 
      p.x[ 1 ] = q->x[ 1 ]; 
      Point dp = point2DrawingAreaPoint( pCtxt, p );
      drawPoint( cr, dp.x[ 0 ], dp.x[ 1 ], 3 );
      Point hd2 = hd;
      hd2.x[ a ] = q->x[ a ];
      Point bg2 = bg;
      bg2.x[ a ] = q->x[ a ];
      viewerKDTree( pCtxt, cr, Gauche( N ), bg, hd2, b );
      viewerKDTree( pCtxt, cr, Droit( N ), bg2, hd, b );
    }
}

On l'appelle ainsi dans expose_evt_reaction :

Point bg = { {-10.0, -10.0} };
Point hd = { { 10.0,  10.0} };
viewerKDTree( pCtxt, cr, Racine( pCtxt->kdtree ), bg, hd, 0 );

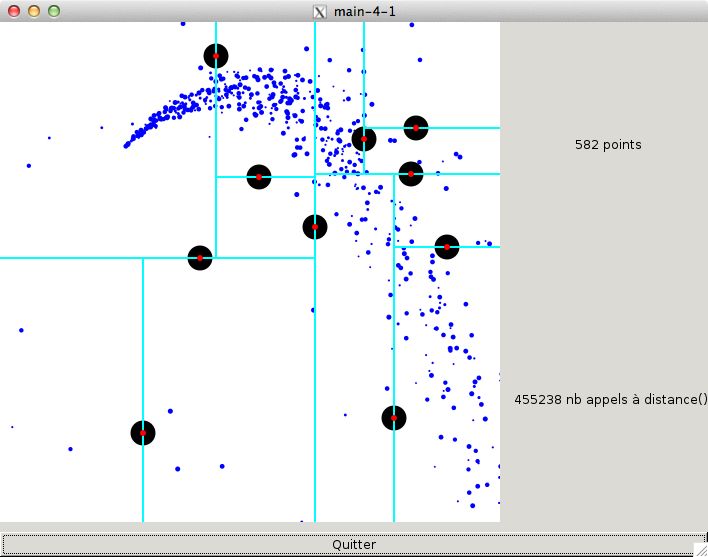
Vous obtenez alors ce genre de résultat, si votre fonction de création d'arbre k-D fonctionne !

Visualisation de l'arbre k-D des obstacles.

4.2 - Détection des obstacles proches de vos particules

Vous êtes presque au bout de vos peines. Il s'agit maintenant juste d'être un peu plus intelligent dans la fonction deplaceParticule, en n'appelant la fonction distance que sur les obstacles suffisamment près de la particule. On va donc utiliser l'algorithme PointsDansBoule vu en-cours et de prototype :

// Ajoute dans le tableau d'obstacles F les obstacles de l'arbre
// désigné par le noeud racine N qui sont à une distance inférieure à
// r du point p. Le paramètre a désigne l'axe courant (0 ou 1) et
// change à chaque niveau de récursion.
void KDT_PointsDansBoule( TabObstacles* F, Noeud* N, Point* p, double r, int a );

Algorithme de recherche des points proches (dans une boule de centre p et de rayon r).

Ensuite, dans deplaceParticule, on ne teste que les obstacles qui ont été détectés par KDT_PointsDansBoule. Une partie du code est donné ci-dessous:

void deplaceParticule( Contexte* pCtxt, Particule* p )
{
  // Déplace p en supposant qu'il n'y a pas de collision.
  Point pp;
  pp.x[ 0 ] = p->x[ 0 ] + DT * p->v[ 0 ];
  pp.x[ 1 ] = p->x[ 1 ] + DT * p->v[ 1 ];
 
  TabObstacles F; // obstacles potentiels;
  TabObstacles_init( &F );
  // Trouve les obstacles dans un rayon de 0.05 du point d'intérêt pp.
  KDT_PointsDansBoule( &F, Racine( pCtxt->kdtree ), &pp, 0.05, 0 );
  // On teste si il y a une "vraie" collision dans F 
  // ...
  // et on déplace le point en fonction
  // ...
  TabObstacles_termine( &F ); // pour éviter les fuites mémoire.
}

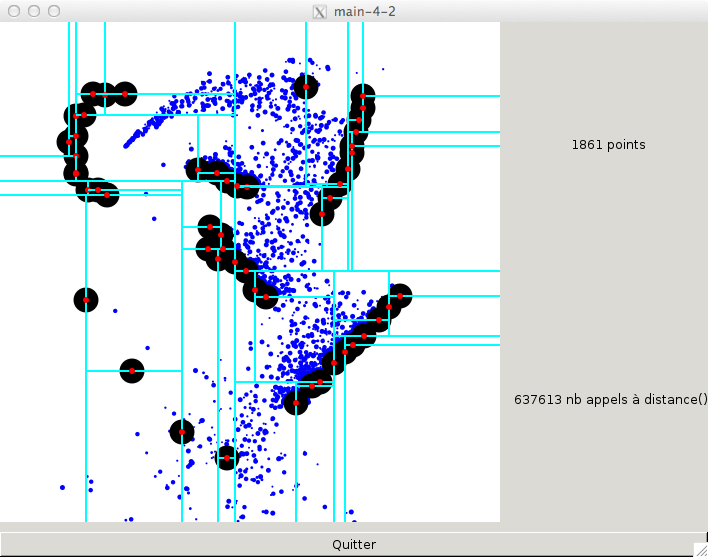
On note qu'ici on a choisi le même rayon de localisation 0.05 que la taille des obstacles. En fait, il faut juste veiller à ce que le rayon d'un obstacle soit inférieur ou égal à ce rayon de localisation. Au bout du compte, votre application ressemble à ceci. On note qu'il y a beaucoup moins d'appels à la fonction distance par seconde, alors même qu'il y a plus de particules et plus d'obstacles !

Visualisation de l'arbre k-D des obstacles et accélération des tests de proximité.

4.3 - Pour aller un peu plus loin

Vous avez toute liberté pour aller un peu plus loin. Le plus dur est fait. On peut s'amuser à étoffer simplement l'application de beaucoup de façons:

mettre d'autres fontaines.
rajouter une couleur aux particules et les colorer différemment selon les fontaines.
laisser l'utilisateur placer plusieurs sortes d'obstacles: des obstacles plus petits ou plus gros, des obstacles avec forte atténuation (att = 0.1) ou au contraire des "bumpers" comme dans les flippers (att=1.5).
créer d'autres forces, comme un attracteur ou un répulseur lorsqu'une particule se rapproche trop d'une zone.
faire des puits qui mangent les particules.
le transformer en jeu avec score et objectifs...
...

On note que gérer les collisions entre particules elles-mêmes est plus délicat, en tous cas avec les arbres k-D. Il faut en effet recréer les arbres stockant les particules à chaque itération.

5 - Remise du tp

Ce TP peut être fait par binôme.
Vous m'enverrez par email votre TP avant le 25 avril 2023 minuit, via TPLab. Il faudra une archive nommée TP3-[votre ou vos nom(s)] contenant tous les fichiers sources, entêtes, makefile.
Bien entendu, il faut que vos programmes compilent sous Linux.
si je fais make, ça doit compiler sans erreur et sans warning (dans vos sources).
Vous me ferez un petit compte-rendu (README) précisant l'état d'avancement (ce qui marche, ce qui marche à moitié, et ce qui ne marche pas), ainsi que les éléments supplémentaires éventuels que vous avez rajoutés.

Table of Contents