1 - Objectifs

L'objectif de ce TP est de vous faire mettre en oeuvre des algorithmes efficaces pour calculer l'enveloppe convexe d'un ensemble de points.

Pour faciliter la visualisation, on utilisera la bibliothèque GTK (http://www.gtk.org) comme interface graphique. Elle permet de tracer des points et des lignes, d'avoir des boutons et sélecteur de paramètres, etc. Vous vous en êtes déjà servi en cours de C, INFO504 (https://www.lama.univ-savoie.fr/pagesmembres/lachaud/Cours/INFO504/Tests/doc/html/tp3.html) pour le TP Tetris graphique.

Pour vous faire gagner du temps, on vous donne une application de base convex.c , qui tire aléatoirement dix points dans le disque unité et affiche tous les points dans une zone de dessin.

Prenez d'abord le temps de bien comprendre le code écrit, le source est consultable là: convex.c, points.h, points.c et est présent dans l'archive, le makefile est ci-dessous:

CC=gcc
LD=gcc
CFLAGS=-g -Wall -Werror -pedantic -std=c11
LIBS=-lm
# gtk+-2.0 pour GTK2
# gtk+-3.0 pour GTK3 (choisi ici)
GTKCFLAGS:=-g $(shell pkg-config --cflags gtk+-3.0)
GTKLIBS:=$(shell pkg-config --libs gtk+-3.0)
 
all: convex
 
convex: convex.o points.o
        $(LD) convex.o points.o $(GTKLIBS) $(LIBS) -o convex
 
convex.o: convex.c
        $(CC) -c $(CFLAGS) $(GTKCFLAGS) convex.c -o convex.o
 
points.o: points.c points.h 
        $(CC) -c $(CFLAGS) $(GTKCFLAGS) points.c -o points.o
 
clean:
        rm -f convex convex.o points.o
 
fullclean: clean
        rm -f *~ *.fig.bak

Il s'exécute ainsi:

prompt$ make
prompt$ ./convex

A l'issue de ce TP, vous aurez:

créer des tableaux dynamiques pour faire une pile de taille arbitraire,
programmer deux algorithmes efficaces de calcul d'enveloppe convexe,
mesurer leurs temps d'exécution et vérifier expérimentalement leur comportement lorsque le nombre de points tend vers l'infini mais aussi en fonction de la distribution spatiale des points.

2 - Nombre de points quelconques et génération aléatoire

Nous allons tester nos fonctions de calcul de l'enveloppe convexe sur des ensembles de points de grande taille, mais aussi de formes particulières. On observera que l'efficacité de certains algorithmes ne dépend pas seulement de la taille des données en entrées, mais aussi de leurs valeurs (ici les formes considérées). Il faut donc d'une part pouvoir traiter des ensembles de points de taille arbitraire mais aussi générer des points suivant différentes formes. C'est ce que l'on fait dans cette section.

2.1 - Tableau de points dynamique

Pour le moment, les fonctions du fichier points.c ne permettent de gérer qu'un tableau de 100 points maximum. Vous pouvez le vérifier en cliquant plusieurs fois sur le bouton pour ajouter des points. Au bout d'un moment, les points ne sont plus ajoutés.

Ecrivez une fonction TabPoints_agrandir, appelée automatiquement par TabPoints_ajoute, qui double la capacité du tableau lorsqu'il est saturé. Notez que vous avez vu en TD que cette opération a un coût amorti constant.

2.2 - Variation du nombre de points ajouté.

Ajoutez un champ GTK_ENTRY pour que l'utilisateur puisse changer le nombre de points ajoutés lorsqu'il clique sur le bouton "Points aléatoires dans disque". Vous utiliserez les fonctions gtk_entry_new puis gtk_entry_set_text et gtk_entry_get_text pour ce faire. Vous ajouterez aussi un champ GTK_LABEL pour afficher le nombre total de points dans le tableau de points. Les fonctions utiles associées sont gtk_label_new et gtk_label_set_text.

Note: Pour converter une chaîne de caractères vers un entier, on rappelle que vous disposez de la fonction int atoi( char * ) dans stdlib.h. Pour faire l'inverse, on peut utiliser sprintf qui affiche dans un tableau de caractères.

char* txt = "357";
int   nb  = atoi( txt );  // nb = 357
char  str[ 100 ];
sprintf( str, "%d", nb ); // str = "357"

2.3 - Génération de points aléatoires dans un losange

Ajoutez un bouton pour générer des points dans le losange de sommets \( \pm (1,0), \pm (0,1) \). L'idée est de tourner les points générés dans le carré \( [-1:1] \times [-1:1] \) de 45 degrés, en divisant les longueurs pour obtenir un côté de taille \(\frac{\sqrt{2}}{2}\). Si x et y sont les coordonnées du point tiré aléatoirement dans le carré précédent, alors la transformation s'écrit ainsi

\[ \left(\begin{array}{c}x'\\ y'\end{array}\right) = \frac{\sqrt{2}}{4} \left(\begin{array}{cc}1&1\\-1&1\end{array}\right) \left(\begin{array}{c}x\\ y\end{array}\right). \]

Vous reconnaissez une rotation de 45 degrés avec un changement d'échelle.

A la fin de cette section, votre application peut ressembler à cela:

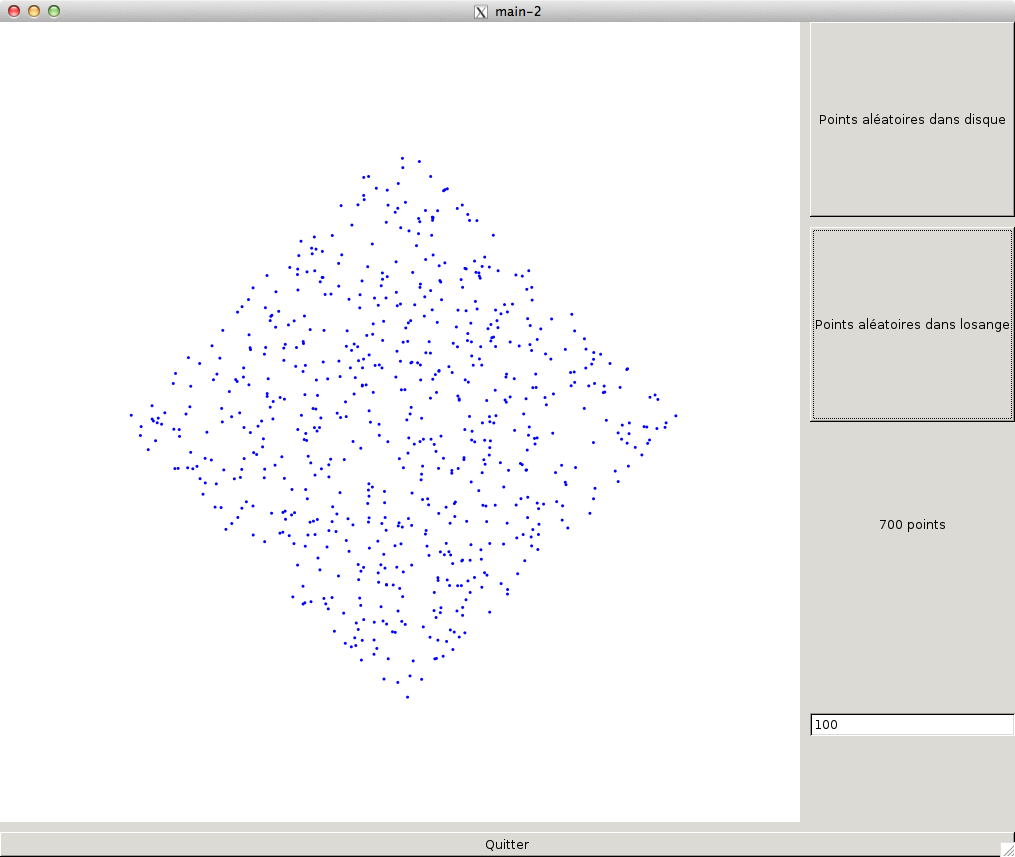
700 points générés aléatoirement dans le losange unité.

3 - Balayage de Graham

Le balayage de Graham suit l'idée suivante. On se donne un point que l'on sait sur l'enveloppe convexe. Ensuite on ordonne tous les points autour selon leur angle polaire par rapport à ce point. On les trie donc suivant cet ordre. Si on considère la ligne polygonale qui relie tous ces points ordonnés, on remarque qu'il s'agit d'un polygone simple.

Balayage de Graham. Les points triés forment un polygone simple.

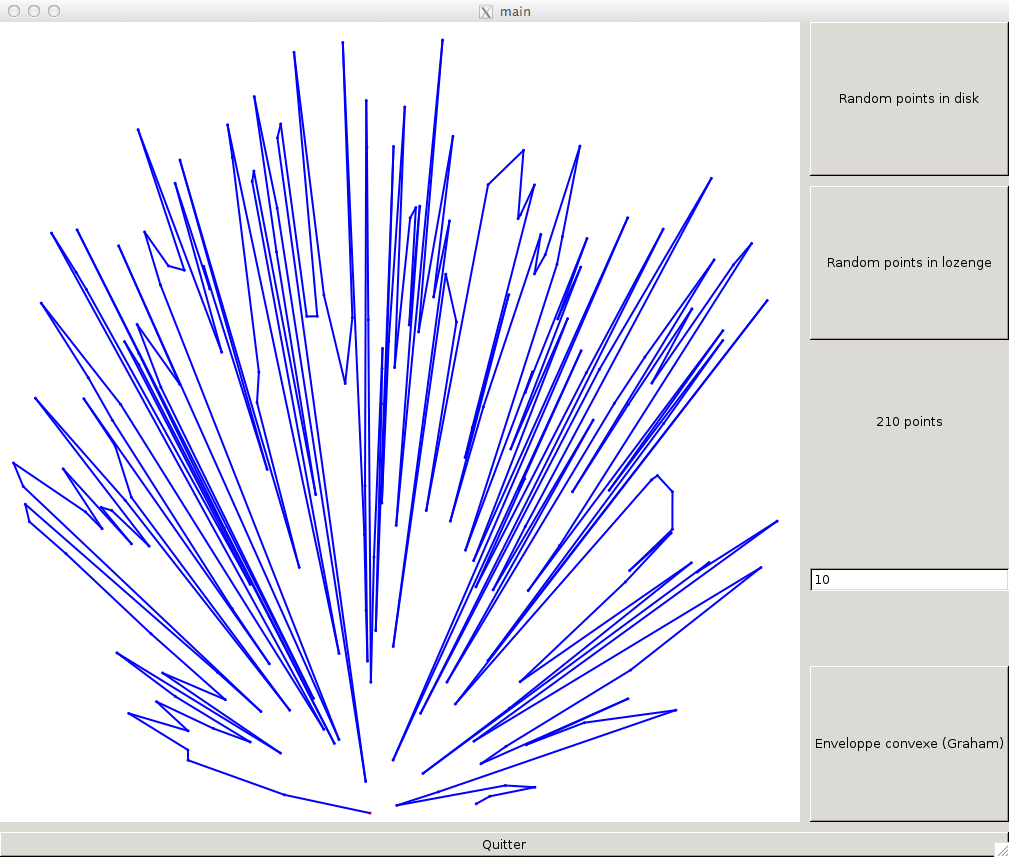
Ensuite il suffit de construire progressivement l'enveloppe convexe à l'aide d'une pile, en vérifiant si le nouveau point ajouté est bien à gauche des deux points précédents sur la pile. Si oui, on l'ajoute à la pile. Si non, on enlève le sommet de pile jusqu'à ce que le point soit bien à gauche des deux précédents. L'algorithme est le suivant.

// Enveloppe convexe par Parcours de Graham.
Procedure ConvexHull(E T : Tableau de Point, E n : entier, S P : Pile de Point);
Var i : entier;
Debut
  i <- TrouverPointBasGauche( T, n );
  Echange( T[0], T[i] ); // T[0] est le pivot
  TrierSelonT0( T, n );  // On trie les points 1 à n-1 suivant l'angle T[0]T[i].
  CréerPile( P );
  Empiler( P, T[ 0 ] );
  Empiler( P, T[ 1 ] );
  Pour i de 2 a n-1 Faire
    Tant que non EstAGauche( ValeurDeuxième( P ), ValeurSommet( P ), T[ i ] ) Faire
      Dépiler( P );
    Empiler( P, T[ i ] );
  // P contient la liste des sommets de l'enveloppe convexe dans l'ordre inverse.
Fin

Notez que vous pouvez utiliser la fonction Orientation vue en cours pour trier les points (plutôt que de vraiment calculer un angle polaire).

3-1 - Recherche du point le plus bas

Dans un premier temps écrivez la fonction qui recherche l'indice du point le plus en bas, et si égalité, le plus à gauche. Ecrivez donc la fonction suivante dans les fichiers points.h et points.c :

int TabPoints_indexBasGauche( TabPoints* tab );

STabPoint

Definition points.h:9

3-2 - Tri du tableau de points

Ecrivez ensuite la fonction de tri suivant l'angle polaire par rapport au point d'indice 0 du tableau tab donné en entrée.

void TabPoints_triSelonT0( TabPoints* tab );

Vous pouvez utiliser votre propre algorithme de tri (bulle, quick sort). On peut aussi utiliser la fonction qsort de stdlib.h en veillant à lui fournir la bonne fonction de comparaison. Faites

prompt$ man 3 qsort

pour avoir des infos.

Note: On doit trier par rapport à la position du point T[0]. Donc il faut passer cette information à la fonction de comparaison de l'algorithme qsort. La solution la plus simple (que vous allez suivre ici) est de définir une variable globale de type Point à laquelle vous affectez la valeur T[0], puis vous pouvez l'utilisez dans la fonction de comparaison appelée par qsort.

3-3 - Structure de Pile

Nous avons besoin d'une structure de pile pour l'algorithme. En récupérant pas mal de code de la structure TabPoints, écrivez une structure de pile de taille quelconque avec les fonctions suivantes:

#ifndef _PILE_H_
#define _PILE_H_
 
#include "points.h"
 
typedef struct SPilePoint {
  int taille;
  int nb;
  Point* points;
} PilePoints;
 
void  PilePoints_init( PilePoints* pile );
int   PilePoints_estVide( PilePoints* pile );
void  PilePoints_empile( PilePoints* pile, Point p );
void  PilePoints_depile( PilePoints* pile );
Point PilePoints_sommet( PilePoints* pile );
// Récupère l'élément juste sous le sommet de la pile.
Point PilePoints_deuxiemeSommet( PilePoints* pile );
void  PilePoints_agrandir( PilePoints* pile );
void  PilePoints_termine( PilePoints* pile );
int   PilePoints_nb( PilePoints* pile );
Point PilePoints_get( PilePoints* pile, int idx );
 
#endif

3-4 - Balayage de Graham

Vous avez maintenant tout ce qu'il faut pour écrire le balayage de Graham (cf. algorithme au dessus). Vous rajouterez un bouton pour réalisez le balayage de Graham. Vous enrichissez la structure Contexte avec une PilePoints qui contiendra le résultat. Pour l'affichage, on peut utiliser la fonction suivante pour afficher une ligne:

void drawLine( cairo_t* cr, Point p, Point q )
{
  cairo_move_to( cr, p.x, p.y );
  cairo_line_to( cr, q.x, q.y );
  cairo_stroke( cr );
}

Voilà maintenant le résultat du balayage de Graham sur un nuage de points dans un disque.

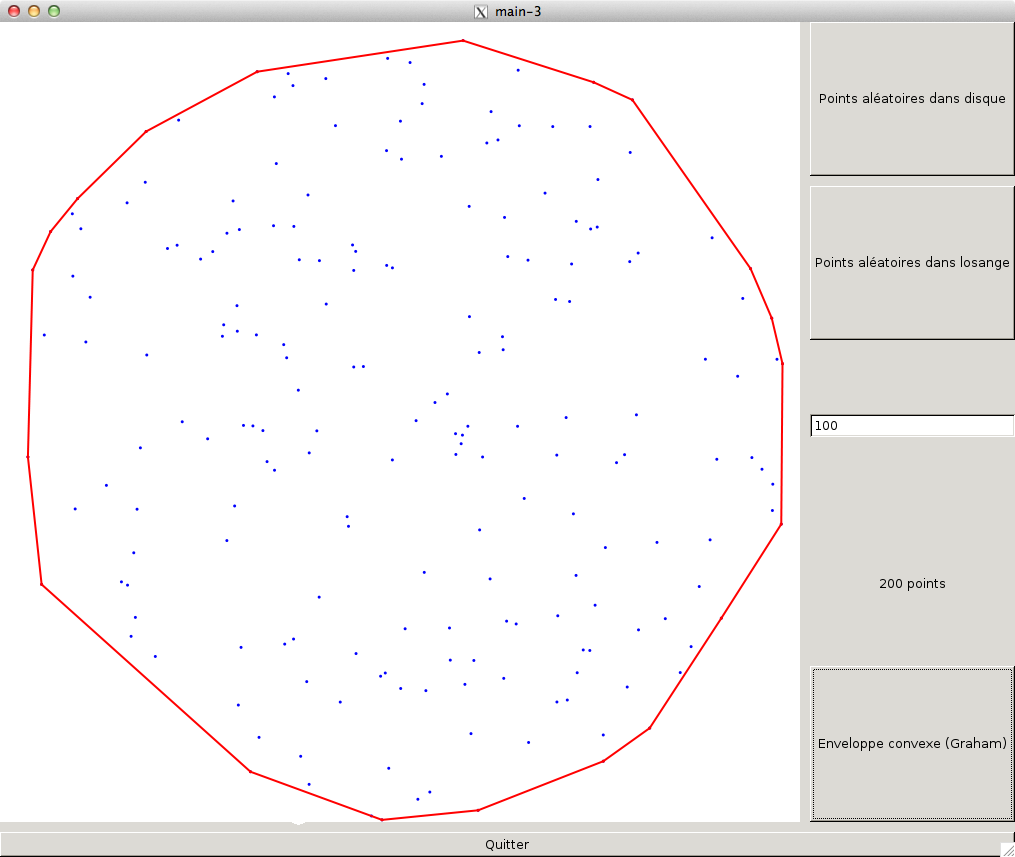
Balayage de Graham. Résultat du calcul de l'enveloppe convexe.

3-5 - Nombre de points et temps d'exécution

En utilisant des GTK_LABEL, affichez maintenant le nombre de points sur l'enveloppe convexe ainsi que le temps d'exécution du dernier calcul de l'enveloppe convexe. On voit ainsi que sur les formes polygonales, l'enveloppe convexe a très peu de sommets.

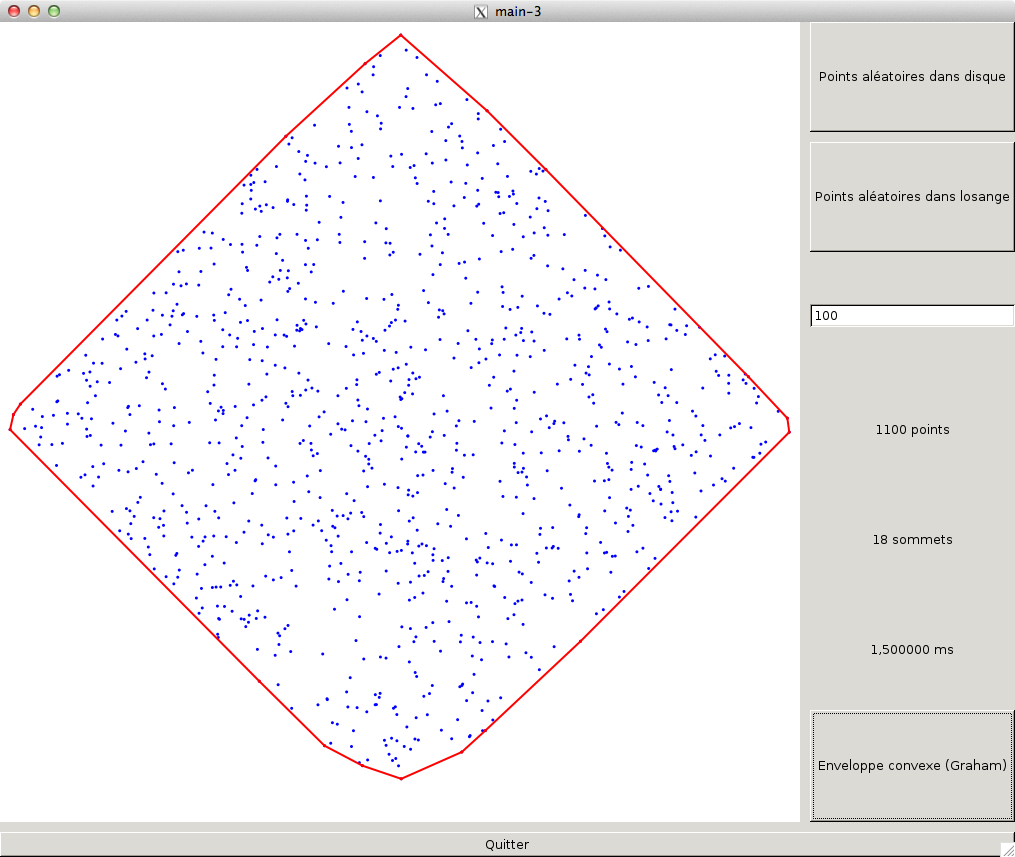
Balayage de Graham. Nombre de sommets de l'enveloppe convexe et temps d'exécution.

Pour mesurer le temps d'exécution, reportez vous au TP précédent (3.3 Utilisation de cette structure pour le découpage en composantes connexes.).

Avec gnuplot par exemple, vous tracerez les courbes suivantes en log-scale afin de mesurer l'efficacité de vos algorithmes ainsi que le nombre de sommets. Prenez un nombre suffisant d'échantillons.

nb de sommets enveloppe convexe en fonction du nombre de points (points dans disque)
temps d'exécution Graham en fonction du nombre de points (points dans disque)
nb de sommets enveloppe convexe en fonction du nombre de points (points dans losange)
temps d'exécution Graham en fonction du nombre de points (points dans losange)

Pour le disque, déterminer (empiriquement) la puissance a tel que \( s = n^a \), où s est le nombre de sommets et n le nombre de points.

Pour le losange qu'observez-vous ?

4 - Algorithme de Jarvis

L'algorithme de Jarvis est en un sens plus simple que l'algorithme de Graham et, dans certains cas, peut être plus rapide. Sa complexité dépend de la sortie du problème, ici du nombre de sommets \( s \) de l'enveloppe convexe. Plus précisément, la complexité est dans \( \Theta(n s) \). L'idée est extrêmement simple. On construit d'abord la partie droite de l'enveloppe convexe. On part du sommet le plus bas. Puis on recherche parmi tous les autres points plus haut le sommet qui a l'angle polaire le plus faible par rapport au point initial. Il fait donc aussi partie de l'enveloppe convexe. On procède de la même manière ensuite en recherchant le sommet plus haut qui a l'angle polaire le plus faible par rapport au deuxième point. Et ainsi de suite jusqu'au sommet le plus haut de l'enveloppe convexe. Pour la partie gauche de l'enveloppe convexe, on procède similairement.

Il est clair qu'un tel algorithme prend un temps \( \Theta(n) \) pour chaque sommet de l'enveloppe convexe. D'où la complexité globale.

Note: On pourrait mesurer l'angle polaire. En fait on cherche le sommet de coordonnée y plus grande qui est toujours à droite des segments orientés partant du sommet précédent de l'enveloppe convexe. On peut donc utiliser Orientation aussi. Comme on ne peut que chercher un point plus haut que le précédent, on coupe la construction de l'enveloppe convexe en partie gauche et droite.

Implémentez l'algorithme de Jarvis. Il devrait être assez lent sur la forme "disque" et être le plus efficace sur la forme "losange".

Vous tracerez les courbes suivantes en log-scale afin de mesurer l'efficacité de vos algorithmes. Prenez un nombre suffisant d'échantillons.

temps d'exécution Jarvis en fonction du nombre de points (points dans disque)
temps d'exécution Jarvis en fonction du nombre de points (points dans losange)

5 - Remise du tp

Ce TP peut être fait par binôme.
Vous m'enverrez votre première version du TP à la fin de la séance, puis la version finale au plus tard dimanche 7 avril 2023 minuit, via TPLab. Il faudra une archive nommée TP2-[votre ou vos nom(s)] contenant tous les fichiers sources, entêtes, makefile.
Vous devez inclure un petit compte-rendu précisant l'état d'avancement (ce qui marche, ce qui marche à moitié, et ce qui ne marche pas), qui donnera les graphiques demandés, et qui pourra montrer quelques exemples de calcul d'enveloppe convexe.
Bien entendu, il faut que vos programmes compilent sous Linux.

Table of Contents