
Robust and Convergent Curvature and Normal Estimators with Digital Integral Invariants
Jan 1, 2017
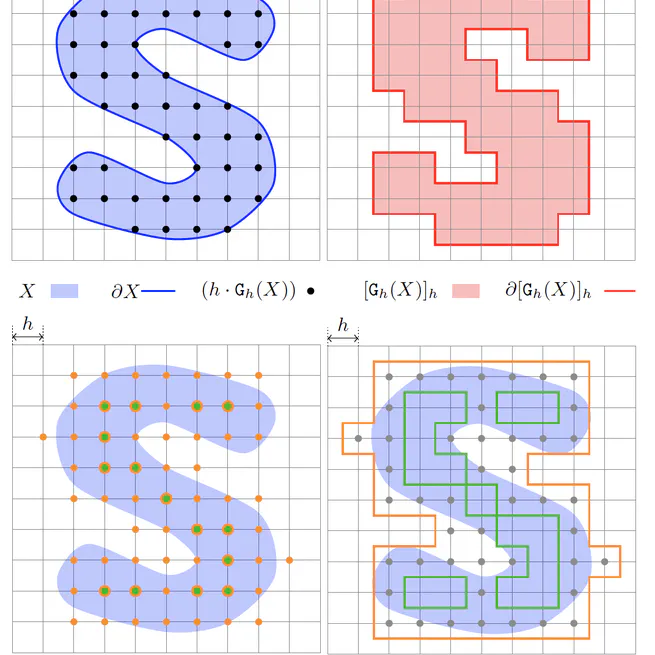
Convergent Geometric Estimators with Digital Volume and Surface Integrals
Keynote speaker at DGCI 2016, Nantes.
Apr 18, 2016
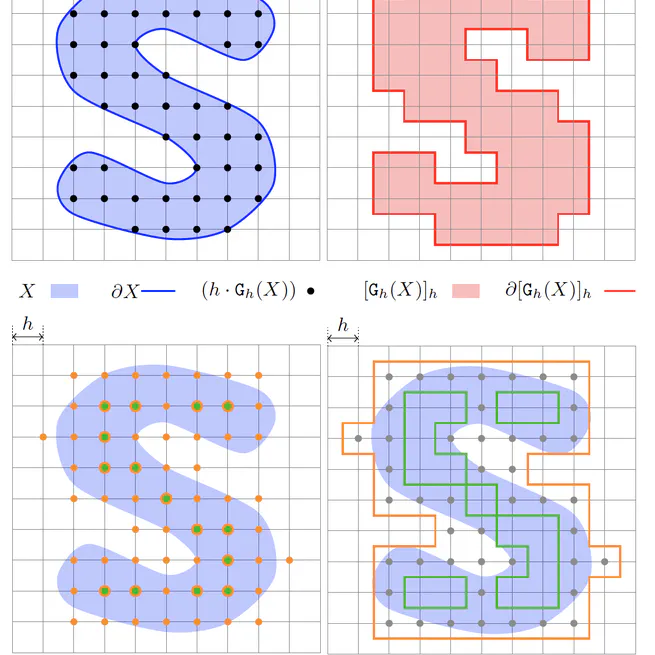
Convergent Geometric Estimators with Digital Volume and Surface Integrals
Jan 1, 2016
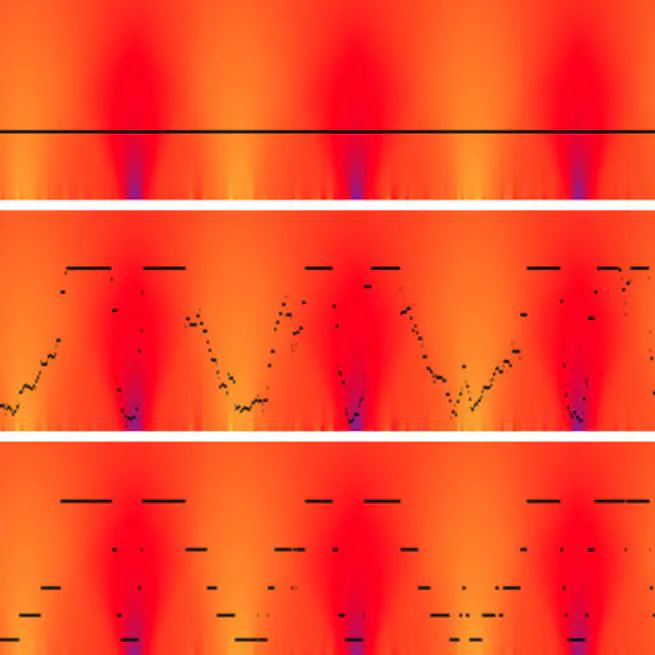
Parameter-Free and Multigrid Convergent Digital Curvature Estimators
Jan 1, 2014
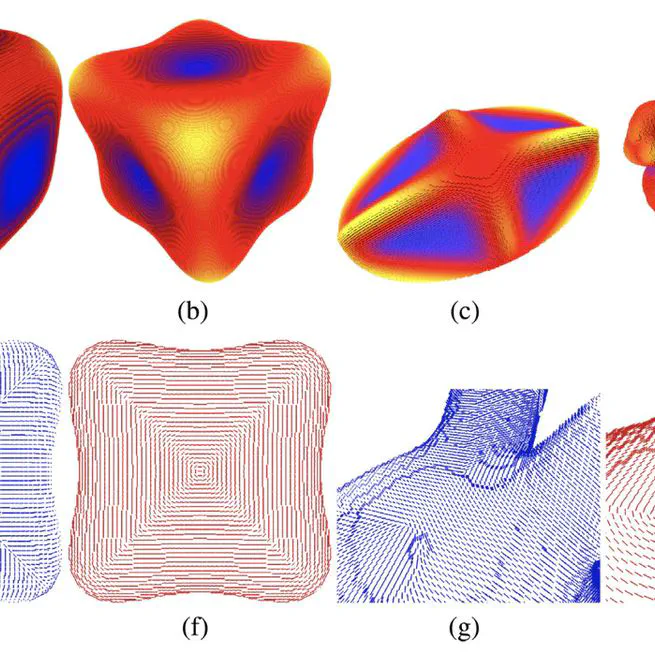
Multigrid convergent principal curvature estimators in digital geometry
Jan 1, 2014
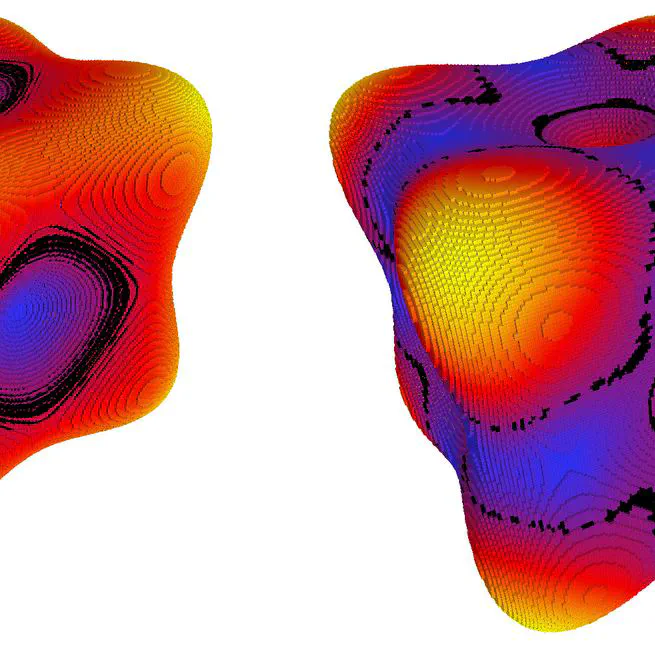
Integral based Curvature Estimators in Digital Geometry
Jan 1, 2013