Full convexity: new characterisations and applications

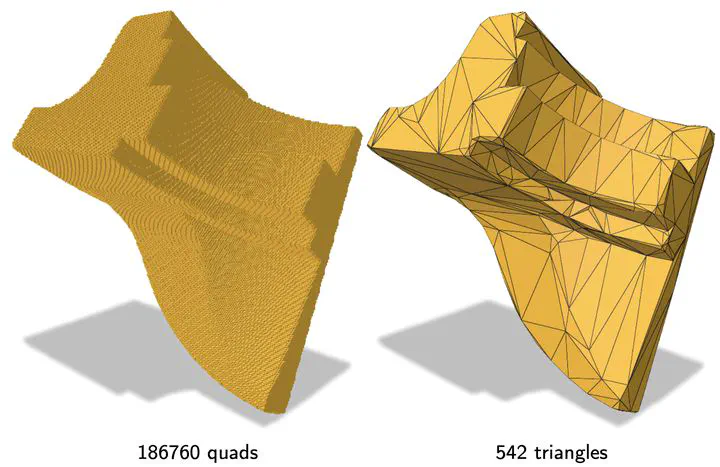
Full convexity was proposed recently as a sound alternative to classical digital convexity. Indeed, it guarantees in arbitrary dimension d the connectedness (and even the simple connectedness) of fully convex sets, while keeping a rich geometry. For instance digital planes and half-spaces are fully convex. We present here several new results and several open problems related to full convexity. One drawback of full convexity is that it require 2^d convex hull computations and lattice point enumerations. We show here that one convex hull computation and enumeration is enough to check full convexity. We then present two new possible characterisations of full convexity. We then focus on the computation of fully convex objects from digital objects and present two alternatives to the already presented fully convex enveloppe. If time permits it, we will conclude with an application of full convexity to polyhedrization of digital sets.

May 15, 2023 9:30 AM — May 17, 2023 12:30 PM