Around global and local convexity in digital spaces

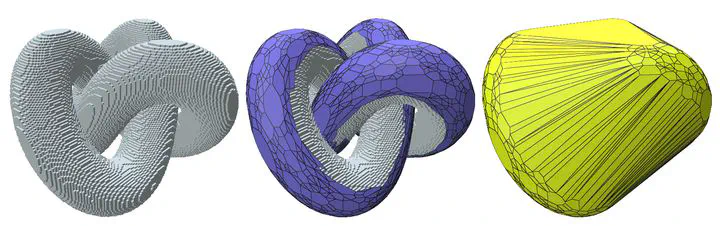
This talk presents several aspects of convexity in digital spaces Z^{d. We first examine the geometry of the digitization of convex shapes and, more precisely determine how the convex hull of these lattice points is close to the geometry of the convex shape before digitization. Under some smoothness properties, we establish that the convex hull is Hausdorff close to the original shape proportionnaly to the digitization gridstep h. Convex hull vertices are shown to be much closer to the shape than expected (proportional to h}(2d/(d+1))). This explains why the convex hull is an appealing reconstruction of digital convex objects. We then show that the normal vector to the convex hull facets converges to the normal vectors of the smooth convex shape with a speed proportional to sqrt(h), and the bound is tight. Secondly we study how we can define the notion of local convexity without recourse to differential geometry. The problem is decomposed into two stages: (i) identification of locally extremal points using a plane-probing variant, (ii) joining pairs of extremal points whenever the straight segment between them stays sufficiently close to the input surface without crossing it (visibility). Finally, convex and concave polyhedral approximations are computed from the previously obtained soup of candidate edges. The method output is exactly the convex hull of the input surface if it is digitally convex and is composed of polyhedral approximations of the convex and concave parts otherwise.

May 7, 2025 9:00 AM — 10:00 AM