Maximal digital straight segments and convergence of discrete geometric estimators
Abstract
Discrete geometric estimators approach geometric quantities on digitized shapes without any knowledge of the continuous shape. A classical yet difficult problem is to show that an estimator asymptotically converges toward the true geometric quantity as the resolution increases. We study here, on Convex Digital Polygons, the convergence of local estimators based on Digital Straight Segment (DSS). This problem is closely linked to the asymptotic growth of maximal DSS, for which we show bounds both about their number and sizes. These results not only give better insights about digitized curves but indicate that curvature estimators based on local DSS recognition are not likely to converge. We indeed invalidate a conjecture which was essential in the only known convergence theorem of a discrete curvature estimator. The proof involves results from arithmetic properties of digital lines, digital convexity, combinatorics, continued fractions and random polytopes.
Type
Publication
Journal of Mathematical Image and Vision, 27(2): 471–502, 2007
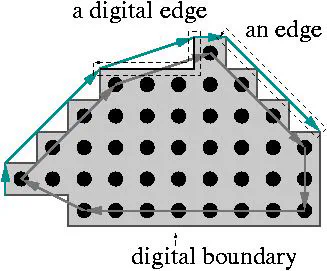
Digital Straightness
Digital Contour
Digital Straight Segment
Tangential Cover
Convex Hull
Lattice Polytope
Multigrid Convergence
Asymptotic Geometry
Curvature Estimation
2D
Authors
Professor of Computer Science
My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.