Mumford-Shah Mesh Processing using the Ambrosio-Tortorelli Functional

Abstract

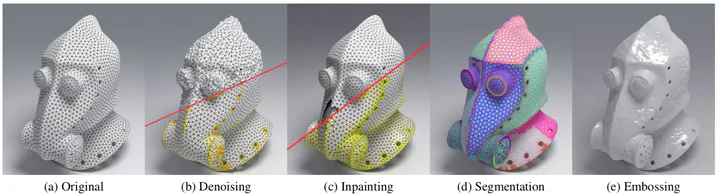
The Mumford-Shah functional approximates a function by a piecewise smooth function. Its versatility makes it ideal for tasks such as image segmentation or restoration, and it is now a widespread tool of image processing. Recent work has started to investigate its use for mesh segmentation and feature lines detection, but we take the stance that the power of this functional could reach far beyond these tasks and integrate the everyday mesh processing toolbox. In this paper, we discretize an Ambrosio-Tortorelli approximation via a Discrete Exterior Calculus formulation. We show that, combined with a new shape optimization routine, several mesh processing problems can be readily tackled within the same framework. In particular, we illustrate applications in mesh denoising, normal map embossing, mesh inpainting and mesh segmentation.

Jacques-Olivier Lachaud

Professor of Computer Science

My research interests include digital geometry, geometry processing, image analysis, variational models and discrete calculus.